Motion of a small black hole

5.4 Motion of a small black hole

5.4.1 Matched asymptotic expansions

The derivation of the MiSaTaQuWa equations of motion presented in Section 5.3 was framed within the paradigm introduced in Sections 5.1 and 5.2 to describe the motion of a point scalar charge, and a point electric charge, respectively. While this paradigm is well suited to fields that satisfy linear wave equations, it is not the best conceptual starting point in the nonlinear context of general relativity. The linearization of the Einstein field equations with respect to the small parameter $m$ did allow us to use the same mathematical techniques as in Sections 5.1 and 5.2, but the validity of the perturbative method must be critically examined when the gravitational potentials are allowed to be singular. So while Equation (550 ) does indeed give the correct equations of motion when $m$ is small, its previous derivation leaves much to be desired. In this section I provide another derivation that is entirely free of conceptual and technical pitfalls. Here the point mass will be replaced by a nonrotating black hole, and the perturbation’s singular behaviour on the world line will be replaced by a well-behaved metric at the event horizon. We will use the powerful technique of matched asymptotic expansions [35 , 32 , 58 , 19 , 1 , 20 ].

The problem presents itself with a clean separation of length scales, and the method relies entirely on this. On the one hand we have the length scale associated with the small black hole, which is set by its mass $m$ . On the other hand we have the length scale associated with the background spacetime in which the black hole moves, which is set by the radius of curvature $ℛ$ ; formally this is defined so that a typical component of the background spacetime’s Riemann tensor is equal to $2 1∕ ℛ$ up to a numerical factor of order unity. We demand that $m ∕ℛ ≪ 1$ . As before we assume that the background spacetime contains no matter, so that its metric is a solution to the Einstein field equations in vacuum.

For example, suppose that our small black hole of mass $m$ is on an orbit of radius $b$ around another black hole of mass $M$ . Then $∘ ----- ℛ ∼ b b∕M > b$ and we take $m$ to be much smaller than the orbital separation. Notice that the time scale over which the background geometry changes is of the order of the orbital period $∘ ----- b b∕M ∼ ℛ$ , so that this does not constitute a separate scale. Similarly, the inhomogeneity scale – the length scale over which the Riemann tensor of the background spacetime changes – is of order $b ∼ ℛ ∘M---∕b < ℛ$ and also does not constitute an independent scale. (In this discussion we have considered $b∕M$ to be of order unity, so as to represent a strong-field, fast-motion situation.)

Figure 10:

A black hole, represented by the black disk, is immersed in a background spacetime. The internal zone extends from $r = 0$ to $r = ri ≪ ℛ$ , while the external zone extends from $r = re ≫ m$ to $r = ∞$ . When $m ≪ ℛ$ there exists a buffer zone that extends from $r = re$ to $r = ri$ . In the buffer zone $m ∕r$ and $r∕ℛ$ are both small.

Let $r$ be a meaningful measure of distance from the small black hole, and let us consider a region of spacetime defined by $r < ri$ , where $ri$ is a constant that is much smaller than $ℛ$ . This inequality defines a narrow world tube that surrounds the small black hole, and we shall call this region the internal zone (see Figure 10 ). In the internal zone the gravitational field is dominated by the black hole, and the metric can be expressed as

where $g(black hole)$ is the metric of a nonrotating black hole in isolation (as given by the unperturbed Schwarzschild solution), while $H1$ and $H2$ are corrections associated with the conditions in the external universe. The metric of Equation (555

) represents a black hole that is distorted by the tidal gravitational field of the external universe, and $H1$ , $H2$ are functions of $m$ and the spacetime coordinates that can be obtained by solving the Einstein field equations. They must be such that the spacetime possesses a regular event horizon near $r = 2m$ , and such that $g(internal zone)$ agrees with the metric of the external universe – the metric of the background spacetime in the absence of the black hole – when $r ≫ m$ . As we shall see in Section 5.4.2, $H1$ actually vanishes and the small correction $H ∕ℛ2 2$ can be obtained by employing the well-developed tools of black-hole perturbation theory [51

, 59

, 63

Consider now a region of spacetime defined by $r > re$ , where $re$ is a constant that is much larger than $m$ ; this region will be called the external zone (see Figure 10 ). In the external zone the gravitational field is dominated by the conditions in the external universe, and the metric can be expressed as

where $g(background spacetime)$ is the unperturbed metric of the background spacetime in which the black hole is moving, while $h1$ and $h2$ are corrections associated with the hole’s presence; these are functions of $ℛ$ and the spacetime coordinates that can be obtained by solving the Einstein field equations. We shall truncate Equation (556

) to first order in $m$ , and $mh1$ will be calculated in Section 5.4.3 by linearizing the field equations about the metric of the background spacetime. In the external zone the perturbation associated with the presence of a black hole cannot be distinguished from the perturbation produced by a point particle of the same mass, and $mh 1$ will therefore be obtained by solving Equation (493

) in the background spacetime.

The metric $g(external zone)$ returned by the procedure described in the preceding paragraph is a functional of a world line $γ$ that represents the motion of the small black hole in the background spacetime. Our goal is to obtain a description of this world line, in the form of equations of motion to be satisfied by the black hole; these equations will be formulated in the background spacetime. It is important to understand that fundamentally, $γ$ exists only as an external-zone construct: It is only in the external zone that the black hole can be thought of as moving on a world line; in the internal zone the black hole is revealed as an extended object and the notion of a world line describing its motion is no longer meaningful.

Equations (555 ) and (556 ) give two different expressions for the metric of the same spacetime; the first is valid in the internal zone $r < ri ≪ ℛ$ , while the second is valid in the external zone $r > re ≫ m$ . The fact that $ℛ ≫ m$ allows us to define a buffer zone in which $r$ is restricted to the interval $r < r < r e i$ . In the buffer zone $r$ is simultaneously much larger than $m$ and much smaller than $ℛ$ – a typical value might be $√ ---- m ℛ$ – and Equations (555 , 556 ) are simultaneously valid. Since the two metrics are the same up to a diffeomorphism, these expressions must agree. And since $g(external zone)$ is a functional of a world line $γ$ while $g(internal zone )$ contains no such information, matching the metrics necessarily determines the motion of the small black hole in the background spacetime. What we have here is a beautiful implementation of the general observation that the motion of self-gravitating bodies is determined by the Einstein field equations.

It is not difficult to recognize that the metrics of Equations (555 , 556 ) can be matched in the buffer zone. When $r ≫ m$ in the internal zone, the metric of the unperturbed black hole can be expanded as $2 2 g(black hole) = η ⊕ m ∕r ⊕ m ∕r ⊕ ...$ , where $η$ is the metric of flat spacetime (in asymptotically inertial coordinates) and the symbol $⊕$ means “and a term of the form…”. On the other hand, dimensional analysis dictates that $H1 ∕ℛ$ be of the form $r∕ℛ ⊕ m ∕ℛ ⊕ m2 ∕(rℛ ) ⊕ ...$ while $H2 ∕ℛ2$ should be expressed as $r2∕ℛ2 ⊕ mr ∕ℛ2 ⊕ m2 ∕ℛ2 ⊕ ...$ . Altogether we obtain

2 2 g(buffer zone) = η ⊕ m ∕r ⊕ m ∕r ⊕ ... ⊕ r∕ℛ ⊕ m∕ ℛ ⊕ m2 ∕(rℛ ) ⊕ ... 2 2 2 2 2 ⊕ r ∕ℛ ⊕ mr ∕ℛ ⊕ m ∕ℛ ⊕ ... ⊕ ... (557 )

for the buffer-zone metric. If instead we approach the buffer zone from the opposite side, letting $r$ be much smaller than $ℛ$ in the external zone, we have that the metric of the background spacetime can be expressed as $g(background spacetime) = η ⊕ r∕ ℛ ⊕ r2∕ℛ2 ⊕ ...$ , where the expansion now uses world-line based coordinates such as the Fermi normal coordinates of Section 3.2 or the retarded coordinates of Section 3.3. On dimensional grounds we also have $2 mh1 = m ∕r ⊕ m ∕ℛ ⊕ mr ∕ℛ ⊕ ...$ and $2 2 2 2 2 2 m h2 = m ∕r ⊕ m ∕(r ℛ) ⊕ m ∕ℛ ⊕ ...$ . Altogether this gives

g(buffer zone) = η ⊕ r∕ℛ ⊕ r2∕ℛ2 ⊕ ... 2 ⊕ m ∕r ⊕ m ∕ℛ ⊕ mr ∕ℛ ⊕ ... ⊕ m2 ∕r2 ⊕ m2 ∕(rℛ ) ⊕ m2 ∕ℛ2 ⊕ ... ⊕ ... (558 )

for the buffer-zone metric. Apart from a different ordering of terms, the metrics of Equations (557

) and (558

) have identical forms.

Matching the metrics of Equations (555 ) and (556 ) in the buffer zone can be carried out in practice only after performing a transformation from the external coordinates used to express $g(external zone)$ to the internal coordinates employed for $g (internal zone)$ . The details of this coordinate transformation will be described in Section 5.4.4, and the end result of matching – the MiSaTaQuWa equations of motion – will be revealed in Section 5.4.5.

5.4.2 Metric in the internal zone

To flesh out the ideas contained in the previous Section 5.4.1 we first calculate the internal-zone metric and replace Equation (555 ) by a more concrete expression. We recall that the internal zone is defined by $r < r ≪ ℛ i$ , where $r$ is a suitable measure of distance from the black hole.

We begin by expressing $g(black hole)$ , the Schwarzschild metric of an isolated black hole of mass $m$ , in terms of retarded Eddington–Finkelstein coordinates $(¯u,¯r,θ¯A )$ , where $¯u$ is retarded time, $¯r$ the usual areal radius, and $¯θA = (θ¯, ¯φ)$ are two angles spanning the two-spheres of constant $¯u$ and $¯r$ . The metric is given by

where $d¯Ω2 = Ω¯AB d¯θAd ¯θB = dθ¯2 + sin2 ¯θ d¯φ2$ is the line element on the unit two-sphere. In the limit $r ≫ m$ this metric achieves the asymptotic values

g¯u¯u → − 1, g¯u¯r = − 1, g¯u¯A = 0, g¯A¯B = r¯2 ¯ΩAB;

these are appropriate for a black hole immersed in a flat spacetime charted by retarded coordinates.

The corrections $H1$ and $H2$ in Equation (555 ) encode the information that our black hole is not isolated but in fact immersed in an external universe whose metric becomes $g(background spacetime )$ asymptotically. In the internal zone the metric of the background spacetime can be expanded in powers of $¯r∕ℛ$ and expressed in a form that can be directly imported from Section 3.3. If we assume for the moment that the “world line” $¯r = 0$ has no acceleration in the background spacetime (a statement that will be justified shortly), then the asymptotic values of $g (internal zone)$ must be given by Equations (210 , 211 , 212 , 213 ):

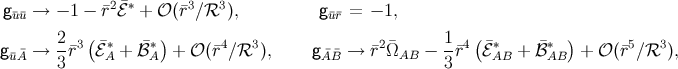
g ¯u¯u → − 1 − ¯r2¯ℰ∗ + 𝒪 (¯r3∕ℛ3 ), g¯u¯r = − 1, g ¯→ 2-¯r3(¯ℰ∗ + ℬ¯∗) + 𝒪 (¯r4∕ℛ3 ), g ¯¯ → r¯2Ω¯ − 1¯r4(ℰ¯∗ + ℬ¯∗ ) + 𝒪 (¯r5∕ℛ3 ), ¯uA 3 A A A B AB 3 AB AB

where

and

are the tidal gravitational fields that were first introduced in Section 3.3.8. Recall that $¯Ωa = (sin ¯θcos ¯φ,sin ¯θ sin ¯φ,cosθ¯)$ and $¯ΩaA = ∂¯Ωa ∕∂¯θA$ . Apart from an angular dependence made explicit by these relations, the tidal fields depend on $¯u$ through the frame components $ℰ ≡ R = 𝒪 (1∕ℛ2 ) ab a0b0$ and $ℬa ≡ 1ɛacdR = 𝒪 (1∕ℛ2 ) b 2 0bcd$ of the Riemann tensor. (This is the Riemann tensor of the background spacetime evaluated at $¯r = 0$ .) Notice that we have incorporated the fact that the Ricci tensor vanishes at $¯r = 0$ : The black hole moves in a vacuum spacetime.

The modified asymptotic values lead us to the following ansatz for the internal-zone metric:

g¯u¯u = − f [1 + r¯2e1(¯r)ℰ¯∗] + 𝒪 (¯r3∕ℛ3 ), (562 ) g¯u¯r = − 1, (563 ) 2- 3[ ¯∗ ¯∗] 4 3 g¯u¯A = 3 ¯r e2(¯r)ℰA + b2(¯r)ℬA + 𝒪 (¯r ∕ℛ ), (564 ) 1 [ ] gA¯¯B = ¯r2¯ΩAB − --¯r4 e3(¯r)¯ℰ∗AB + b3(¯r) ¯ℬA∗B + 𝒪 (¯r5∕ ℛ3). (565 ) 3

The five unknown functions $e1$ , $e2$ , $e3$ , $b2$ , and $b3$ can all be determined by solving the Einstein field equations; they must all approach unity when $r ≫ m$ and be well-behaved at $r = 2m$ (so that the tidally distorted black hole will have a nonsingular event horizon). It is clear from Equations (562

, 563

, 564

, 565

) that the assumed deviation of $g(internal zone )$ with respect to $g(black hole)$ scales as $2 1∕ℛ$ . It is therefore of the form of Equation (555

) with $H1 = 0$ . The fact that $H1$ vanishes comes as a consequence of our previous assumption that the “world line” $¯r = 0$ has a zero acceleration in the background spacetime; a nonzero acceleration of order $1∕ℛ$ would bring terms of order $1∕ℛ$ to the metric, and $H 1$ would then be nonzero.

Why is the assumption of no acceleration justified? As I shall explain in the next paragraph (and you might also refer back to the discussion of Section 5.3.7), the reason is simply that it reflects a choice of coordinate system: Setting the acceleration to zero amounts to adopting a specific – and convenient – gauge condition. This gauge differs from the Lorenz gauge adopted in Section 5.3, and it will be our choice in this section only; in the following Section 5.4.3 we will return to the Lorenz gauge, and the acceleration will be seen to return to its standard MiSaTaQuWa expression.

Inspection of Equations (560 ) and (561 ) reveals that the angular dependence of the metric perturbation is generated entirely by scalar, vectorial, and tensorial spherical harmonics of degree $ℓ = 2$ . In particular, $H2$ contains no $ℓ = 0$ and $ℓ = 1$ modes, and this statement reflects a choice of gauge condition. Zerilli has shown [63 ] that a perturbation of the Schwarzschild spacetime with $ℓ = 0$ corresponds to a shift in the mass parameter. As Thorne and Hartle have shown [58 ], a black hole interacting with its environment will undergo a change of mass, but this effect is of order $3 2 m ∕ℛ$ and thus beyond the level of accuracy of our calculations. There is therefore no need to include $ℓ = 0$ terms in $H2$ . Similarly, it was shown by Zerilli that odd-parity perturbations of degree $ℓ = 1$ correspond to a shift in the black hole’s angular-momentum parameters. As Thorne and Hartle have shown, a change of angular momentum is quadratic in the hole’s angular momentum, and we can ignore this effect when dealing with a nonrotating black hole. There is therefore no need to include odd-parity, $ℓ = 1$ terms in $H2$ . Finally, Zerilli has shown that in a vacuum spacetime, even-parity perturbations of degree $ℓ = 1$ correspond to a change of coordinate system – these modes are pure gauge. Since we have the freedom to adopt any gauge condition, we can exclude even-parity, $ℓ = 1$ terms from the perturbed metric. This leads us to Equations (562 , 563 , 564 , 565 ), which contain only $ℓ = 2$ perturbation modes; the even-parity modes are contained in those terms that involve $ℰab$ , while the odd-parity modes are associated with $ℬab$ . The perturbed metric contains also higher multipoles, but those come at a higher order in $1∕ℛ$ ; for example, the terms of order $3 1∕ ℛ$ include $ℓ = 3$ modes. We conclude that Equations (562 , 563 , 564 , 565 ) is a sufficiently general ansatz for the perturbed metric in the internal zone.

There remains the task of finding the functions $e1$ , $e2$ , $e3$ , $b2$ , and $b3$ . For this it is sufficient to take, say, $ℰ12 = ℰ21$ and $ℬ12 = ℬ21$ as the only nonvanishing components of the tidal fields $ℰab$ and $ℬab$ . And since the equations for even-parity and odd-parity perturbations decouple, each case can be considered separately. Including only even-parity perturbations, Equations (562 )–(565 ) become

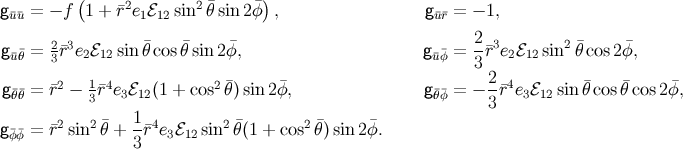
g = − f (1 + r¯2e ℰ sin2 ¯θsin2φ¯), g = − 1, ¯u¯u 1 12 ¯u¯r 2 3 ¯ ¯ ¯ 2- 3 2 ¯ ¯ g¯u¯θ = 3¯r e2ℰ12sin θcosθ sin 2φ, g¯u¯φ = 3 ¯r e2ℰ12 sin θcos 2φ, 2 1 4 2 ¯ ¯ 2-4 ¯ ¯ ¯ g¯θ¯θ = ¯r − 3¯r e3ℰ12(1 + cos θ)sin2φ, g¯θ¯φ = − 3¯r e3ℰ12 sin θcos θcos2 φ, 2 2 1 4 2 2 g¯φ¯φ = ¯r sin θ¯+ --¯r e3ℰ12sin ¯θ(1 + cos ¯θ) sin 2¯φ. 3

This metric is then substituted into the vacuum Einstein field equations, $G αβ = 0$ . Calculating the Einstein tensor is simplified by linearizing with respect to $ℰ 12$ and discarding its derivatives with respect to $¯u$ : Since the time scale over which $ℰab$ changes is of order $ℛ$ , the ratio between temporal and spatial derivatives is of order $¯r∕ℛ$ and therefore small in the internal zone; the temporal derivatives can be consistently neglected. The field equations produce ordinary differential equations to be satisfied by the functions $e1$ , $e2$ , and $e3$ . Those are easily decoupled, and demanding that the functions all approach unity as $r → ∞$ and be well-behaved at $r = 2m$ yields the unique solutions

Switching now to odd-parity perturbations, Equations (562

, 563

, 564

, 565

) become

g ¯u¯u = − f g¯u¯r = − 1, g ¯= − 2-¯r3b2ℬ12sinθ¯cos2φ¯, g ¯ = 2-¯r3b2ℬ12sin2 ¯θ cos ¯θ sin 2¯φ, ¯uθ 3 ¯uφ 3

2 1 g ¯θθ¯= ¯r2 + --¯r4b3ℬ12 cosθ¯cos2φ¯, g¯θ¯φ = − --¯r4b3ℬ12 sin ¯θ(1 + cos2 ¯θ) sin 2¯φ, 3 3

2 g¯φ¯φ = ¯r2sin2 ¯θ −--¯r4b3ℬ12 sin2 ¯θcos ¯θcos 2¯φ. 3

Following the same procedure, we arrive at

Substituting Equations (566

) and (567

) into Equations (562

, 563

, 564

, 565

) returns our final expression for the metric in the internal zone.

It shall prove convenient to transform $g(internal zone )$ from the quasi-spherical coordinates $(¯r, ¯θA)$ to a set of quasi-Cartesian coordinates $a ¯ a ¯A ¯x = ¯rΩ (θ )$ . The transformation rules are worked out in Section 3.3.7 and further illustrated in Section 3.3.8. This gives

( ) g¯u¯u = − f 1 + ¯r2f ¯ℰ∗ + 𝒪 (¯r3∕ℛ3 ), (568 ) ( ) g¯u¯a = − ¯Ωa + 2¯r2f ¯ℰ∗a + ¯ℬ∗a + 𝒪 (¯r3∕ℛ3 ), (569 ) 3 ( ) ¯ ¯ 1-2 m2- ¯∗ 1- 2 ¯∗ 3 3 g ¯a¯b = δab − ΩaΩb − 3¯r 1 − 2 ¯r2 ℰ ab − 3 ¯r ℬab + 𝒪(¯r ∕ℛ ), (570 )

where $f = 1 − 2m ∕¯r$ and where the tidal fields

¯ℰ∗ = ℰab¯Ωa ¯Ωb, (571 ) ¯∗ ( b ¯ ¯b) ¯ c ℰa = δa − ΩaΩ ℰbcΩ , (572 ) ¯ℰ∗ab = 2ℰab − 2¯Ωa ℰbc¯Ωc − 2¯Ωbℰac¯Ωc + (δab + ¯Ωa¯Ωb )ℰ¯∗, (573 ) ¯∗ ¯b c ¯d ℬa = ɛabcΩ ℬ dΩ( , ) ( ) (574 ) ℬ¯∗ab = ɛacd¯Ωcℬde δeb − ¯Ωe ¯Ωb + ɛbcd¯Ωc ℬde δea − ¯Ωe¯Ωa (575 )

were first introduced in Section 3.3.8. The metric of Equations (568

, 569

, 570

) represents the spacetime geometry of a black hole immersed in an external universe and distorted by its tidal gravitational fields.

5.4.3 Metric in the external zone

We next move on to the external zone and seek to replace Equation (556 ) by a more concrete expression; recall that the external zone is defined by $m ≪ re < r$ . As was pointed out in Section 5.4.1, in the external zone the gravitational perturbation associated with the presence of a black hole cannot be distinguished from the perturbation produced by a point particle of the same mass; it can therefore be obtained by solving Equation (493 ) in a background spacetime with metric $g(background spacetime)$ . The external-zone metric is decomposed as

where $gαβ$ is the metric of the background spacetime and $hαβ = 𝒪 (m )$ is the perturbation; we shall work consistently to first order in $m$ and systematically discard all terms of higher order. We relate $hαβ$ to trace-reversed potentials $γαβ$ ,

and solving the linearized field equations produces

where $zμ(τ)$ gives the description of the world line $γ$ , $τ$ is proper time in the background spacetime, $u μ = dzμ∕dτ$ is the four-velocity, and $G +αβμν(x,z)$ is the retarded Green’s function associated with Equation (493

); the potentials of Equation (578

) satisfy the Lorenz-gauge condition $αβ γ ;β = 0$ . As was pointed out in Section 5.4.1, $γαβ$ (and therefore $hαβ$ ) are functionals of a world line $γ$ that will be determined by matching $g(external zone )$ to $g (internal zone)$ .

We now place ourselves in the buffer zone (where $m ≪ r ≪ ℛ$ and where the matching will take place) and work toward expressing $g(external zone )$ as an expansion in powers of $r∕ℛ$ . For this purpose we will adopt the retarded coordinates $a (u,rΩ )$ of Section 3.3 and rely on the machinery developed there.

We begin with $g αβ$ , the metric of the background spacetime. We have seen in Section 3.3.8 that if the world line $γ$ is a geodesic, if the vectors $eμa$ are parallel transported on the world line, and if the Ricci tensor vanishes on $γ$ , then the metric takes the form given by Equations (207 , 208 , 209 ). This form, however, is too restrictive for our purposes: We must allow $γ$ to have an acceleration, and allow the basis vectors to be transported in the most general way compatible with their orthonormality property; this transport law is given by Equation (138 ),

where $aa(τ) = aμeμ a$ are the frame components of the acceleration vector $aμ = Du μ ∕dτ$ , and $ωab(τ) = − ωba(τ)$ is a rotation tensor to be determined. Anticipating that $aa$ and $ωab$ will both be proportional to $m$ , we express the metric of the background spacetime as

g = − 1 − 2ra Ωa − r2ℰ∗ + 𝒪 (r3∕ℛ3 ), (580 ) uu (a ) gua = − Ωa + r δ b− ΩaΩb ab − rωabΩb + 2-r2(ℰ∗ + ℬ ∗) + 𝒪 (r3∕ℛ3 ), (581 ) a 3 a a 1- 2 ∗ ∗ 3 3 gab = δab − Ωa Ωb − 3r (ℰab + ℬ ab) + 𝒪 (r ∕ℛ ), (582 )

where $∗ ℰ$ , $∗ ℰa$ , $∗ ℰab$ , $∗ ℬ a$ , and $∗ ℬab$ are the tidal gravitational fields first introduced in Section 3.3.8. The metric of Equations (580

, 581

, 582

) is obtained from the general form of Equations (171

, 172

, 173

) by neglecting quadratic terms in $aa$ and $ωab$ and specializing to a zero Ricci tensor.

To express the perturbation $h αβ$ as an expansion in powers of $r∕ ℛ$ we first go back to Equation (498 ) and rewrite it in the form

in which primed indices refer to the retarded point $x′ ≡ z(u)$ associated with $x$ , and

∫ ∫ tail u μ ν τ< μ ν γαβ (x) = 4m Vαβμν(x,z )u u d τ + 4m G+ αβμν(x, z)u u dτ ∫ τ< − − ∞ u μ ν ≡ 4m G+ αβμν(x,z)u u dτ (584 ) −∞

is the “tail part” of the gravitational potentials (recall that $τ<$ is the proper time at which $γ$ enters $x$ ’s normal convex neighbourhood from the past). We next expand the first term on the right-hand side of Equation (583

) with the help of Equation (501

), and the tail term is expanded using Equation (93

) in which we substitute Equation (504

) and the familiar relation $α ′ α′ a α′ σ = − r(u + Ω ea )$ . This gives

where $γtαai′βl′$ is the tensor of Equation (584

) evaluated at $x′$ , and where

was first defined by Equation (545

At this stage we introduce the trace-reversed fields

∫ u− ( 1 ′ ) htaαi′βl′(x′) = 4m G+ α′β′μν − -gα′β′G +δδ′μν (x′,z)uμu ν dτ, (587 ) − ∞ ( 2 ) tail ′ ∫ u− 1 δ′ ′ μ ν hα′β′γ′(x ) = 4m ∇ γ′ G+ α′β′μν − --gα′β′G + δ′μν (x ,z)u u dτ (588 ) − ∞ 2

and recognize that the metric perturbation obtained from Equations (577

) and (585

) is

This is the desired expansion of the metric perturbation in powers of $r∕ ℛ$ . Our next task will be to calculate the components of this tensor in the retarded coordinates $(u,rΩa)$ .

The first step of this computation is to decompose $hαβ$ in the tetrad $α α (e0,ea)$ that is obtained by parallel transport of $′ ′ (u α,eαa )$ on the null geodesic that links $x$ to its corresponding retarded point $x ′ ≡ z(u)$ on the world line. (The vectors are parallel transported in the background spacetime.) The projections are

a α β 2m-- tail [ tail tail c] 2 3 h00(u,r,Ω ) ≡ h αβe0e0 = r + h 00 (u) + r h000(u) + h00c(u )Ω + 𝒪 (mr ∕ℛ ), (590 ) a α β tail [ tail tail c] 2 3 h0b(u,r,Ω ) ≡ h αβe0eb = h0b (u) + r h0b0(u ) + h 0bc(u)Ω + 𝒪 (mr ∕ℛ ), (591 ) a α β 2m-- tail [ tail tail c] 2 3 hab(u,r,Ω ) ≡ h αβeaeb = r δab + hab (u) + r hab0(u ) + h abc(u)Ω + 𝒪 (mr ∕ℛ ); (592 )

on the right-hand side we have the frame components of $tail hα′β′$ and $tail hα′β′γ′$ taken with respect to the tetrad $′ ′ (uα ,eαa )$ ; these are functions of retarded time $u$ only.

The perturbation is now expressed as

hαβ = h00e0e0 + h0b(e0 eb+ ebe0) + habeaeb, α β α β α β α β

and its components are obtained by involving Equations (169 ) and (170 ), which list the components of the tetrad vectors in the retarded coordinates; this is the second (and longest) step of the computation. Noting that $aa$ and $ωab$ can both be set equal to zero in these equations (because they would produce negligible terms of order $m2$ in $h αβ$ ), and that $Sab$ , $Sa$ , and $S$ can all be expressed in terms of the tidal fields $ℰ ∗$ , $ℰa∗$ , $ℰa∗b$ , $ℬ∗a$ , and $ℬ ∗ab$ using Equations (204 , 205 , 206 ), we arrive at

2m-- tail ( ∗ tail tail a) 2 3 huu = r + h 00 + r 2m ℰ + h000 + h00aΩ + 𝒪 (mr ∕ℛ ), (593 ) 2m [ 2m ] hua = ----Ωa + ht0aail+ Ωaht0a0il+r 2m ℰ∗Ωa + ---(ℰa∗+ ℬ ∗a) + hta0ai0l+ Ωahta0i0l0 + ht0aailbΩb + Ωahta0i0lbΩb r 3 + 𝒪(mr2 ∕ℛ3 ), (594 ) hab = 2m--(δab + Ωa Ωb) + Ωa Ωbht0a0il+ Ωahta0ibl+ Ωbhta0ial+ htaaibl r [ 2m-- ∗ ∗ ∗ ∗ ∗ ∗ ( tail tail c) + r − 3 (ℰ ab + Ωa ℰb + ℰaΩb + ℬ ab + Ωa ℬb + Ωbℬ a) + Ωa Ωb h000 + h 00cΩ ] + Ω (htail+ htailΩc ) + Ω (htail + htailΩc) + (htail+ htailΩc ) + 𝒪(mr2 ∕ℛ3 ). (595 ) a 0b0 0bc b 0a0 0ac ab0 abc

These are the coordinate components of the metric perturbation $hαβ$ in the retarded coordinates $a (u,rΩ )$ , expressed in terms of frame components of the tail fields $tails hα′β′$ and $tails hα′β′γ′$ . The perturbation is expanded in powers of $r∕ℛ$ and it also involves the tidal gravitational fields of the background spacetime.

The external-zone metric is obtained by adding $gαβ$ as given by Equations (580 , 581 , 582 ) to $hαβ$ as given by Equations (593 , 594 , 595 ). The final result is

g = − 1 − r2ℰ∗ + 𝒪(r3∕ℛ3 ) uu + 2m--+ htail+ r(2m ℰ∗ − 2a Ωa + htail + htailΩa) + 𝒪 (mr2 ∕ℛ3 ), (596 ) r 00 a 000 00a 2- 2 ∗ ∗ 3 3 gua = − Ωa + 3 r (ℰa + ℬa) + 𝒪 (r ∕ℛ ) 2m + ----Ωa + ht0aail+ Ωaht0a0il r[ ] ∗ 2m-- ∗ ∗ ( b b) b tail tail tail b tail b + r 2m ℰ Ωa + 3 (ℰa+ ℬa)+ δa − Ωa Ω ab− ωabΩ +h 0a0+ Ωah 000+h 0abΩ + Ωah 00bΩ 2 3 + 𝒪 (mr ∕ℛ ), (597 ) 1- 2 ∗ ∗ 3 3 gab = δab − Ωa Ωb − 3 r (ℰab + ℬ ab) + 𝒪 (r ∕ℛ ) 2m tail tail tail tail + ----(δab + Ωa Ωb) + Ωa Ωbh00 + Ωah 0b + Ωbh0a + h ab r[ + r − 2m-(ℰ ∗+ Ω ℰ ∗+ ℰ ∗Ω + ℬ∗ + Ω ℬ ∗+ Ω ℬ ∗) + Ω Ω (htail+ htailΩc) 3 ab a b a b ab a b b a a b 000 00c ( ) ( ) ( )] + Ωa ht0aibl0 + ht0abilcΩc + Ωb ht0aail0 + ht0aialcΩc + htaaib0l+ htaabilcΩc + 𝒪 (mr2 ∕ℛ3 ). (598 )

Because $hta′ils′ α β$ is of order $m ∕ℛ$ and $hta′ils′′ α βγ$ of order $m ∕ℛ2$ , we see that the metric possesses the buffer-zone form $2 2 2 g = η ⊕ r ∕ℛ ⊕ m ∕r ⊕ m ∕ℛ ⊕ mr ∕ℛ$ that was anticipated in Equation (558

). Notice that the expansion adopted here does not contain a term at order $r∕ℛ$ and presumes that $aa$ and $ωab$ are both of order $m ∕ℛ2$ ; this will be confirmed in Section 5.4.5.

5.4.4 Transformation from external to internal coordinates

Comparison of Equations (568 , 569 , 570 ) and Equations (596 , 597 , 598 ) reveals that the internal-zone and external-zone metrics do no match in the buffer zone. But as the metrics are expressed in two different coordinate systems, this mismatch is hardly surprising. A meaningful comparison of the two metrics must therefore come after a transformation from the external coordinates $(u,rΩa )$ to the internal coordinates $(¯u,¯rΩ¯a )$ . Our task in this section is to construct this coordinate transformation. We shall proceed in three stages. The first stage of the transformation, $a ′ ′ ′a (u, rΩ ) → (u ,rΩ )$ , will be seen to remove unwanted terms of order $m ∕r$ in $g αβ$ . The second stage, $′ ′ ′a ′′ ′′ ′′a (u ,r Ω ) → (u ,r Ω )$ , will remove all terms of order $m ∕ℛ$ in $gα′β′$ . Finally, the third stage $(u′′,r′′Ω ′′a) → (¯u,¯r¯Ωa )$ will produce the desired internal coordinates.

The first stage of the coordinate transformation is

and it affects the metric at orders $m ∕r$ and $2 mr ∕ℛ$ . This transformation redefines the radial coordinate – $′ r → r = r + m$ – and incorporates in $′ u$ the gravitational time delay contributed by the small mass $m$ . After performing the coordinate transformation the metric becomes

g ′′ = − 1 − r ′2ℰ′∗ + 𝒪 (r′3∕ℛ3 ) uu + 2m--+ htail+ r′(4m ℰ′∗ − 2a Ω′a + htail+ htailΩ ′a) + 𝒪 (mr ′2∕ℛ3 ), (601 ) r′ 00 a 000 00a ′ 2- ′2 ′∗ ′∗ ′3 3 gu′a′ = − Ωa + 3r (ℰa + ℬa ) + 𝒪 (r ∕ℛ ) tail ′ tail + h0[a + Ωah 00 ] ′ 4m-- ′∗ ′∗ ( b ′ ′b) ′b tail ′ tail tail ′b ′ tail ′b +r − 3 (ℰa + ℬa ) + δa − ΩaΩ ab − ωabΩ + h0a0 + Ω ah000 + h0abΩ + Ωah 00bΩ ′2 3 + 𝒪 (mr ∕ℛ ), (602 ) ′ ′ 1- ′2 ′∗ ′∗ ′3 3 ga′b′ = δab − Ω aΩb − 3 r (ℰab + ℬab) + 𝒪 (r ∕ℛ ) ′ ′ tail ′ tail ′ tail tail + Ω a[Ωbh00 + Ωah0b + Ωbh0a + hab ′ 2m-- ′∗ ′ ′∗ ′∗ ′ ′∗ ′ ′∗ ′ ′∗ ′ ′( tail tail ′c) + r 3 (ℰab + Ω aℰb + ℰ a Ω b + ℬ ab + Ω aℬb + Ωbℬa ) + Ω aΩ b h000 + h 00cΩ ] + Ω ′(htail+ htailΩ′c) + Ω ′(htail+ htailΩ ′c) + (htail+ htailΩ ′c) a 0b0 0bc b 0a0 0ac ab0 abc + 𝒪 (mr ′2∕ℛ3 ). (603 )

This metric matches $g(internal zone)$ at orders $1$ , $r′2∕ℛ2$ , and $m ∕r′$ , but there is still a mismatch at orders $m ∕ℛ$ and $mr ′∕ℛ2$ .

The second stage of the coordinate transformation is

∫ ′ ′′ ′ 1- u tail ′ ′ 1-′[ tail ′ tail ′ ′a tail ′ ′a ′b] u = u − 2 h 00 (u )du − 2r h 00 (u ) + 2h 0a (u )Ω + h ab (u )Ω Ω , (604 ) 1 x ′′a = x′a + -htaabil(u′)x ′b, (605 ) 2

and it affects the metric at orders $m ∕ℛ$ and $mr ∕ℛ2$ . After performing this transformation the metric becomes

gu′′u′′ = − 1 − r′′2ℰ ′′∗ + 𝒪 (r′′3∕ℛ3 ) 2m [ ( 1 ) ] + --′′-+ r′′ 4m ℰ′′∗ − 2 aa − --ht0ai0la + hta0ai0l Ω ′′a + 𝒪 (mr ′′2∕ℛ3 ), (606 ) r 2 ′′ 2-′′2 ′′∗ ′′∗ ′′3 3 gu′′a′′ = − Ω a + 3r (ℰ a + ℬ a ) + 𝒪 (r ∕ℛ ) [ 4m ( ) ( 1 ) + r′′− ----(ℰ′a′∗ + ℬ′a′∗) − 2m ℰabΩ′′b + δab− Ω ′′aΩ′′b ab − --hta0i0bl+ ht0abil0 − ωabΩ ′′b 3 2 ] 1 ′′ tail 1 tail ′′b tail ′′b 1 ( b ′′ ′′b) tail ′′2 3 + 2Ω ah000 − 2hab0Ω + h0abΩ + 2- δa + Ω aΩ h 00b + 𝒪 (mr ∕ ℛ ), (607 ) g ′′ ′′ = δ − Ω ′′Ω′′− 1-r′′2(ℰ′′∗+ ℬ′′∗) + 𝒪 (r ′′3∕ℛ3 ) a b ab [ a b 3 ab ab ′′ 2m ′′∗ ′′ ′′∗ ′′∗ ′′ ′′∗ ′′ ′′∗ ′′ ′′∗ ′′ ′′( tail tail ′′c) + r ---(ℰab + Ω aℰb + ℰa Ωb + ℬ ab + Ω aℬb + Ω bℬa ) + Ω aΩ b h000 + h00cΩ 3 ] ′′( tail tail ′′c) ′′( tail tail ′′c) ( tail tail ′′c) + Ωa h0b0 + h0bcΩ + Ω b h0a0 + h0acΩ + hab0 + habcΩ ′′2 3 + 𝒪 (mr ∕ℛ ). (608 )

To arrive at these expressions we had to involve the relations

which are obtained by covariant differentiation of Equation (587

) with respect to $u$ . The metric now matches $g(internal zone )$ at orders $1$ , $r ′′2∕ℛ2$ , $m ∕r′′$ , and $m ∕ℛ$ , but there is still a mismatch at order $′′ 2 mr ∕ℛ$ .

The third and final stage of the coordinate transformation is

′′ 1 ′′2[ tail ( tail tail) ′′a ( tail tail) ′′a ′′b tail ′′a ′′b ′′c] ¯u = u − --r h000 + h 00a + 2h0a0 Ω + hab0 + 2h 0ab Ω Ω + habcΩ Ω Ω , (610 ) ( 4m ) ¯xa = 1 + -- r′′ℰbcΩ ′′bΩ′′c x′′a 3[ ( ) ] + 1r′′2 − 1htail+ htail+ htail− htail+ htail+ 4m-ℰ Ω ′′b + (Q − Q + Q )Ω ′′bΩ ′′c, 2 2 00a 0a0 0ab 0ba ab0 3 ab abc bca cab (611 )

where

This transformation puts the metric in its final form

g = − 1 − ¯r2¯ℰ∗ + 𝒪(¯r3∕ℛ3 ) ¯u¯u [ ( ) ] 2m-- ¯∗ 1-tail tail ¯a 2 3 + r¯ + ¯r 4m ℰ − 2 aa − 2h00a + h0a0 Ω + 𝒪 (m ¯r ∕ℛ ), (613 ) 2 ( ) g¯u¯a = − ¯Ωa + --¯r2 ¯ℰ∗a + ℬ¯∗a + 𝒪 (¯r3∕ℛ3 ) [ 3 ( ) ] 4m--(¯∗ ¯∗) ( b ¯ ¯ b) 1-tail tail ( tail) ¯b + ¯r − 3 ℰa + ℬa + δa − Ωa Ω ab − 2h00b + h 0b0 − ωab − h 0[ab] Ω 2 3 + 𝒪 (m ¯r ∕ℛ ), (614 ) ¯ ¯ 1- 2(¯∗ ¯∗ ) 3 3 2 3 g¯a¯b = δab − Ωa Ωb − 3 ¯r ℰab + ℬab + 𝒪 (¯r ∕ℛ ) + 𝒪 (m ¯r ∕ℛ ). (615 )

Except for the terms involving $aa$ and $ωab$ , this metric is equal to $g(internal zone )$ as given by Equations (568

, 569

, 570

) linearized with respect to $m$ .

5.4.5 Motion of the black hole in the background spacetime

A precise match between $g (external zone)$ and $g(internal zone)$ is produced when we impose the relations

and

While Equation (616

) tells us how the black hole moves in the background spacetime, Equation (617

) indicates that the vectors $μ ea$ are not Fermi–Walker transported on the world line.

The black hole’s acceleration vector $μ a μ a = a e a$ can be constructed from the frame components listed in Equation (616 ). A straightforward computation gives

where the tail integral

was previously defined by Equation (588

). These are the MiSaTaQuWa equations of motion, exactly as they were written down in Equation (550

). While the initial derivation of this result was based upon formal manipulations of singular quantities, the present derivation involves only well-behaved fields and is free of any questionable aspect. Such a derivation, based on matched asymptotic expansions, was first provided by Yasushi Mino, Misao Sasaki, and Takahiro Tanaka in 1997 [39

Substituting Equations (616 ) and (617 ) into Equation (579 ) gives the following transport equation for the tetrad vectors:

This can also be written in the alternative form

that was first proposed by Mino, Sasaki, and Tanaka. Both equations state that in the background spacetime, the tetrad vectors are not Fermi–Walker transported on $γ$ ; the rotation tensor is nonzero and given by Equation (617