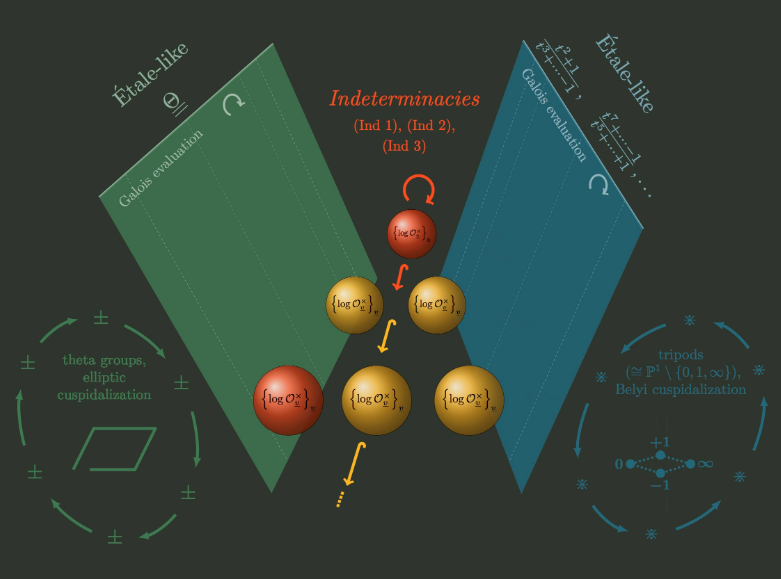
Since its announcement in 2012, Inter-universal Teichmüller theory (IUT),
now well into its second decade, has developed into an important branch of
anabelian geometry, with numerous interconnections to diophantine
geometry, analytic number theory, and anabelian arithmetic geometry.
This
workshop will focus not only, as in previous workshops, on the exposition
of the abundant interconnections between IUT and more classical topics
such as the functional equation of the theta function, analytic
continuation of complex analytic functions, and the p-adic theory of
crystals, but also on exciting new research developments concerning the
relationship between IUT and Galois-Teichmüller theory and the Section Conjecture in anabelian geometry.
In particular, the workshop will include both expository talks for newcomers and talks reporting on recent
research.
Previous IUT Workshops
We include below a list of selected previous workshops on Inter-universal Teichmüller theory. The links given below include lists of speakers and participants, notes, slides, and videos of the talks.
IUGC conference 2024
Organizers: Yuichiro Hoshi (RIMS, Kyoto University), Fumiharu Kato (Tokyo Institute of Technology (PE)), Shinichi Mochizuki (RIMS, Kyoto University).
This workshop was an international research conference held at the Inter-universal Geometry Center (IUGC), Zen University.
Participants: ~60
Inter-universal Teichmüller Theory Summit 2021
Organizers: Shinichi Mochizuki (RIMS), Yuichiro Hoshi (RIMS), Ivan Fesenko (Nottingham), Yuichiro Taguchi (Tokyo Institute of Technology), Benjamin Collas (RIMS/Lille).
This workshop was directed primarily toward advanced learners of the theory, as well as researchers who have already acquired a thorough understanding of the theory. It focused on issues related to the exposition or formulation of the theory from a more advanced point of view, as well as on new research developments related to the theory.
Participants: ~60
Promenade in Inter-Universal Teichmüller Theory 2020-21
Organizers: Benjamin Collas (RIMS/Lille), Pierre Dèbes (Lille), Benoit Fresse (Lille).
This one-semester international seminar was organized by Painlevé-Lille (France) and RIMS-Kyoto (Japan) with the goal of providing an opportunity for arithmetic geometers to gain a general understanding of results, insights, and techniques of IUT. The program was structured around diophantine geometry, IUT, and anabelian geometry.
Participants: ~40
Inter-universal Teichmüller Theory Summit 2016
Organizers: Ivan Fesenko (Nottingham), Shinichi Mochizuki (RIMS), Yuichiro Taguchi (Tokyo Institute of Technology)
The goal of this workshop was to assist mathematicians in their study of IUT, which extends arithmetic geometry to a non-scheme-theoretic setting and, more generally, opens up a fundamentally new area of mathematics. It focused on the presentation and analysis of key principles, concepts, objects, and proofs of IUT and their interconnections with various existing theories.
Participants: ~45
References
- S.Mochizuki. Inter-universal Teichmüller Theory as an Anabelian Gateway to Diophantine Geometry and Analytic Number Theory, in ``MFO–RIMS Tandem Workshop: Arithmetic Homotopy and Galois Theory''. Oberwolfach Rep. 20 (2023), no. 3, pp. 2432–2437 [LINK]
- S.Mochizuki, S.Tsujimura. Resolution of Nonsingularities, Point-theoreticity, and Metric-admissibility for p-adic Hyperbolic Curve, RIMS preprint 1974 (June 2023), revised version: [LINK] (March 2024), 107 pp
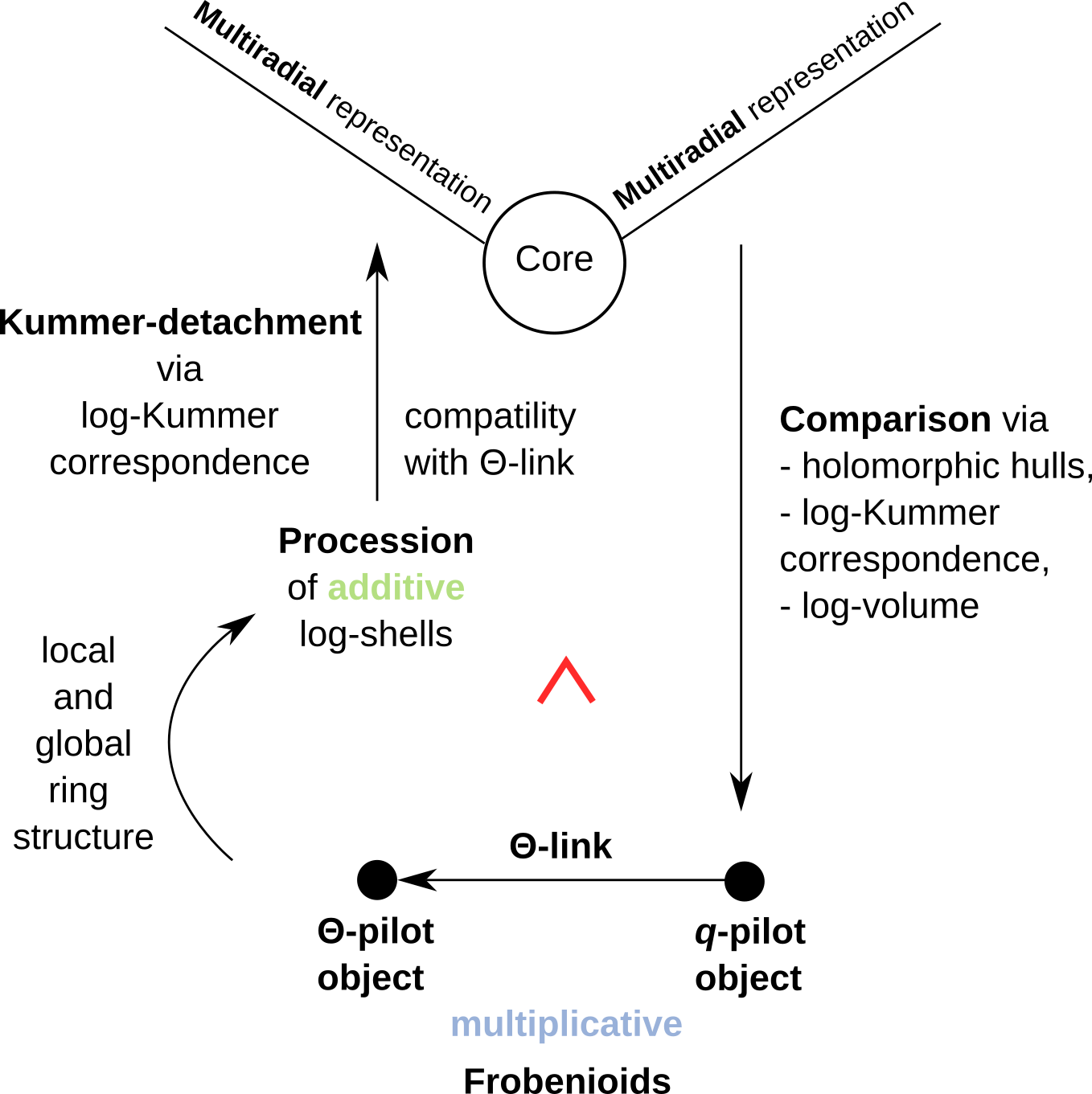
- S.Mochizuki. On the Essential Logical Structure of Inter-universal Teichmüller Theory in Terms of Logical AND "∧"/Logical OR "∨" Relations: Report on the Occasion of the Publication of the Four Main Papers on Inter-universal Teichmüller Theory, RIMS preprint 1968 (Nov. 2022) updated March 2024 [PDF], 167 pp
- S.Mochizuki, I.Fesenko, Y.Hoshi, A.Minamide, W.Porowski. Explicit estimates in inter-universal Teichmüller theory, Kodai Math. J. 45(2): 175-236 (June 2022) [LINK]
- Y.Hoshi, S.Mochizuki, S.Tsujimura. Combinatorial Construction of the Absolute Galois Group of the Field of Rational Numbers, RIMS Preprint 1935 (December 2020), revised version: [LINK] (Jul., 2024), 101 pp
- M.Stoll, Finite descent obstructions and rational points on curves, Algebra Number Theory 1 (4) 349 - 391, 2007 [LINK]