実数データの DCT を計算するもっとも単純な方法は,データの長さを 倍にしてデータを対称にしてから,実数データに対する拡張 FFT で計算する ことです.しかし,これは半分の無駄な計算が含まれます.ここでは, データの対称性を用いて,演算量と記憶領域を実数データの拡張 FFT の 1/2 (複素数データの拡張 FFT の1/4) にする方法について示します [参考文献].
最初に,DCT-II :
N-1
A = Σ a cos(π(j+1/2)k/N) , 0 <= k < N
k j=0 j
は,対称なデータの拡張 DFT :
2N-1
A = Σ b exp(2π(j+1/2)k/2N) , 0 <= k < N
k j=0 j
に相当します.ここで,配列 b は a を対称にしたもので,
1
b = b = --- a , 0 <= j < N
j 2N-1-j 2 j
です.この対称性は,実数データに対する拡張 FFT の log(N) 回ある すべての段のデータに複素共役対称として波及していきます.そして, 最後の段で A_k が A_k 自身の複素共役対称となり,実数に戻ります. この冗長な演算と記憶領域は, 実数データの拡張 FFTの リスト 2.2-2 の拡張 FFT のバタフライループの長さを半分にすることで簡単に 取り除くことができます.
次に,対称性を用いて実数に対する拡張 FFT の演算量と記憶領域を 半分にした DCT-II のルーチンを示します.
| リスト2.3.3-1. 拡張 FFT の冗長な演算を取り除いた FCT-II |
|---|
/*
離散コサイン変換 (Unnormalized DCT-II) :
F[k]=Σ_j=0^n-1 a[j]*cos(pi*(j+1/2)*k/n),0<=k<n を計算する.
*/
#include <math.h>
void fct_ii(int n, double a[])
{
int m, mh, mq, i, j, k, irev, jr, ji, kr, ki;
double theta, wr, wi, xr, xi;
/* ---- scrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
xr = a[j];
a[j] = a[i];
a[i] = xr;
}
}
theta = -4 * atan(1.0) / n;
for (mh = 2; (m = mh << 1) <= n; mh = m) {
mq = mh >> 1;
/* ---- real to real & complex butterflies ---- */
irev = 0;
for (jr = 0; jr < n; jr += m) {
wr = cos(0.5 * theta * (irev + mq));
wi = sin(0.5 * theta * (irev + mq));
for (k = n >> 2; k > (irev ^= k); k >>= 1);
ki = jr + mq;
kr = n - ki;
ji = kr - mq;
xr = a[jr] - a[kr];
xi = -a[ji] + a[ki];
a[jr] += a[kr];
a[ji] += a[ki];
a[ki] = wr * xr + wi * xi;
a[kr] = wr * xi - wi * xr;
}
if (mh == 2) continue;
/* ---- complex to complex butterflies ---- */
irev = 0;
for (i = 0; i < n; i += m) {
wr = cos(theta * (irev + mq));
wi = sin(theta * (irev + mq));
for (k = n >> 2; k > (irev ^= k); k >>= 1);
for (j = 1; j < mq; j++) {
jr = i + j;
ki = i + mh - j;
ji = n - jr;
kr = n - ki;
xr = a[jr] - a[kr];
xi = -a[ji] - a[ki];
a[jr] += a[kr];
a[ji] -= a[ki];
a[ki] = wr * xr + wi * xi;
a[kr] = wr * xi - wi * xr;
}
}
}
if (n > 1) {
m = n >> 1;
xr = a[0] - a[m];
a[0] += a[m];
a[m] = xr * cos(0.5 * theta * m);
}
}
|
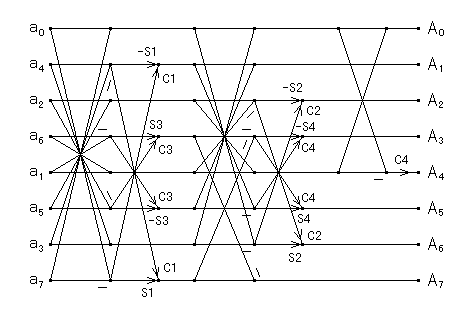
このルーチンの N=8 のときのデータフローは次のようになります.
 |
| 図2.3.3-1. 拡張 FFT の冗長な演算を取り除いた FCT-II |
|---|
次に,この手続きを逆にした DCT-III に対するルーチンを示します.
| リスト2.3.3-2. 拡張 FFT の冗長な演算を取り除いた FCT-III |
|---|
/*
逆離散コサイン変換 (Unnormalized DCT-III) :
a[k]=Σ_j=0^n-1 F[j]*cos(pi*j*(k+1/2)/n),0<=k<n を計算する.
*/
#include <math.h>
void fct_iii(int n, double a[])
{
int m, mh, mq, i, j, k, irev, jr, ji, kr, ki;
double theta, wr, wi, xr, xi;
theta = 4 * atan(1.0) / n;
if (n > 1) {
m = n >> 1;
xr = a[m] * cos(0.5 * theta * m);
a[m] = a[0] - xr;
a[0] += xr;
}
for (m = n; (mh = m >> 1) >= 2; m = mh) {
mq = mh >> 1;
/* ---- real & complex to real butterflies ---- */
irev = 0;
for (jr = 0; jr < n; jr += m) {
wr = cos(0.5 * theta * (irev + mq));
wi = sin(0.5 * theta * (irev + mq));
for (k = n >> 2; k > (irev ^= k); k >>= 1);
ki = jr + mq;
kr = n - ki;
ji = kr - mq;
xr = wr * a[ki] + wi * a[kr];
xi = wr * a[kr] - wi * a[ki];
a[kr] = a[jr] - xr;
a[ki] = a[ji] + xi;
a[jr] += xr;
a[ji] -= xi;
}
if (mh == 2) continue;
/* ---- complex to complex butterflies ---- */
irev = 0;
for (i = 0; i < n; i += m) {
wr = cos(theta * (irev + mq));
wi = sin(theta * (irev + mq));
for (k = n >> 2; k > (irev ^= k); k >>= 1);
for (j = 1; j < mq; j++) {
jr = i + j;
ki = i + mh - j;
ji = n - jr;
kr = n - ki;
xr = wr * a[ki] + wi * a[kr];
xi = wr * a[kr] - wi * a[ki];
a[kr] = a[jr] - xr;
a[ki] = -a[ji] - xi;
a[jr] += xr;
a[ji] -= xi;
}
}
}
/* ---- unscrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
xr = a[j];
a[j] = a[i];
a[i] = xr;
}
}
}
|
この方法は,基数を大きくしたり Split-Radix FFT にしたりすることで, 演算量はさらに減らすことができます.さらに, 混合基数にすることで任意の 長さの DCT が計算できます.
ここでは,Cooley-Tukey 型 FFT と同様の考え方で,長さ N の DCT-II を 二つの N/2 の長さの DCT-II に分解することで導かれる高速コサイン変換を 示します.この考えに基づく高速コサイン変換は B.G. Lee [参考文献] による 高速コサイン変換として知られているようです.
まず,DCT-II :
N-1
A = Σ a cos(π(j+1/2)k/N)
k j=0 j
N-1 (j+1/2)k
= Σ a C , 0 <= k < N
j=0 j N
を次のように分解します.
N/2-1 (j+1/2)k
A = Σ (a + a ) C
2k j=0 j N-1-j N/2
N/2-1 j+1/2 (j+1/2)k
A + A = Σ (a − a )2 C C
2k-1 2k+1 j=0 j N-1-j N N/2
ここで,C は
j
C = cos(πj/N)
N
です.この分解は,基数 2 の周波数間引き FFT の分解と似ていますが, A の奇数の項の分解が異なり,簡単な漸化式になっています.したがって, 通常のバタフライ演算以外に後処理が必要になります.具体的には, まず分解の式に K=0 を代入し,1/2 倍して初項 A_1 を求めます (A_-1 = A_1 という関係から).次に,逐次的に A の奇数項を求めて行きます. この後処理はスケーリングを除外すれば加減算だけで計算できます.しかし, これはバタフライの段数-1 回行わなければなりません.
次に,この方法による DCT-II のルーチンを示します.
| リスト2.3.3-3. B.G. Lee による FCT-II |
|---|
/*
離散コサイン変換 (Unnormalized DCT-II) :
F[k]=Σ_j=0^n-1 a[j]*cos(pi*(j+1/2)*k/n),0<=k<n を計算する.
*/
#include <math.h>
void fct_ii(int n, double a[])
{
int m, mh, i, j, k, irev, j0, j1;
double theta, c2, xr;
/* ---- scrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
xr = a[j];
a[j] = a[i];
a[i] = xr;
}
}
theta = 2 * atan(1.0) / n;
/* ---- butterflies ---- */
for (mh = 1; (m = mh << 1) <= n; mh = m) {
irev = 0;
for (i = 0; i < n; i += m) {
c2 = 2 * cos(theta * (irev + mh));
for (k = n >> 1; k > (irev ^= k); k >>= 1);
for (j = 0; j < mh; j++) {
j0 = i + j;
j1 = n - mh - i + j;
xr = a[j0] - a[j1];
a[j0] += a[j1];
a[j1] = c2 * xr;
}
}
}
/* ---- adds ---- */
for (m = n >> 1; (mh = m >> 1) >= 1; m = mh) {
for (j = 0; j < mh; j++) {
j0 = m + mh + j;
a[j0] = -a[j0] - a[j0 - m];
}
for (i = (m << 1) + mh; i < n; i += (m << 1)) {
for (j = 0; j < mh; j++) {
j0 = i + j;
j1 = j0 + m;
a[j0] -= a[j0 - m];
a[j1] = -a[j1] - a[j0];
}
}
}
/* ---- scaling ---- */
for (j = 1; j < n; j++) {
a[j] *= 0.5;
}
}
|
このルーチンの N=8 のときのデータフローは次のようになります.
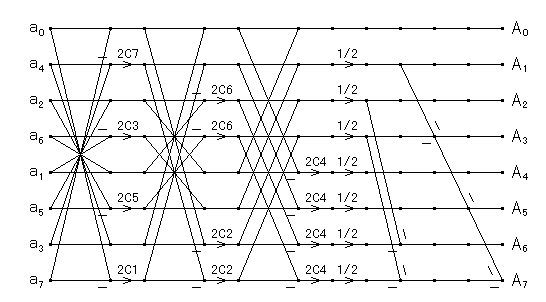 |
| 図2.3.3-2. B.G. Lee による FCT-II |
|---|
次に,演算量について少し考えます.1/2 によるスケーリングは, バタフライ演算の回転因子に含めることができます.したがって, 長さ N の DCT-II の計算に必要な乗算回数 μ と加算回数 α は次のように なります.
N
μ = --- log N
2
3N
α = ---- log N - N + 1
2
この演算量は非常に少なく,拡張 FFT の計算量を半分にする第一の方法に 対して,Split-Radix FFT を用い,さらに複素乗算を 3 回の実数乗算と 3 回の 実数加算で計算したときの演算量に匹敵します.また,この B.G. Lee の方法に 関しても大きい基数や Split-Radix にすれば演算量は減らせると思うかも しれませんが,実際はそう甘くはなく演算量はまったく同じになります. 基数をいじることは,ループ展開による高速化技法としてしか意味を持たなく なります.しかし,二次元 DCT を計算する場合は通常の FFT 同様に,後に示す Vector-Radix FFT を用いれば 乗算回数だけをさらに 3/4 に減らすことが可能になります.
DCT-III に関しても,この手続きを逆にすることで得られます. このとき,前処理は単なる和で直接計算できます.しかし,バタフライの 回転因子には 1/(2*cos(π*j/N)) と除算が入ってしまい,除算を 避けるようにあらかじめ計算しておかなければなりません.
最後に,この方法の欠点を挙げておきます.それは,バタフライ演算と 後処理の漸化式の計算で,長さ N に比例する丸め誤差が入るということです. したがって,あまり大きな計算には向きません.
ここでは,長さ N の DCT-II を一つの N/2 の長さの DCT-II と二つの N/4 の長さの DCT-II に分解することによる高速コサイン変換を示します.
まず,DCT-II :
N-1
A = Σ a cos(π(j+1/2)k/N) , 0 <= k < N
k j=0 j
を次のように N/2 の長さの DCT-II と DCT-IV に分解します.
N/2-1
A = Σ (a + a ) cos(π(j+1/2)k/(N/2))
2k j=0 j N-1-j
N/2-1
A = Σ (a − a )cos(π(j+1/2)(k+1/2)/(N/2))
2k+1 j=0 j N-1-j
次に,N/2 の長さの DCT-IV を 2.3.2 で示した DCT-IV に対する分解を 用いて二つの N/4 の長さの DCT-II にします.この分解を繰り返すことで 高速算法が得られます.このとき同時に,DCT-IV に対する高速算法も 得られます.この高速算法は Split-Radix FFT とよく似た構造で L 字型の バタフライとなり,log(N) 段の演算は一段ずつ終了しなくなります. さらに,加減算からなる後処理が必要で多少複雑になります.また, この方法の演算量は DCT-IV の分解に現れる複素乗算を 3 回の加算と 3 回の乗算に置き換えたとき,B.G. Lee の方法とほぼ同じになります.
この方法の分解は,N 点の DCT を通常の DFT だと思って, Cooley-Tukey 型 FFT の分解を素直に用いたものです.この分解を表にすると 次のようになります.
| リスト2.3.3-4. DCT の分解 | |
|---|---|
| N+1 点 DCT-I | N+1 回の加算により N/2+1 点 DCT-I と N/2 点 DCT-III に分解 |
| N 点 DCT-II | N 回の加算により N/2 点 DCT-II と N/2 点 DCT-IV に分解 |
| N 点 DCT-IV | N-2 回の加算と N/2 回の複素数乗算により二組の N/2 点 DCT-II に分解 |
| N+1 点 DCT-I | N+1 回の加算により N/2+1 点 DCT-I と N/2 点 DCT-II に分解 |
| N 点 DCT-III | N 回の加算により N/2 点 DCT-III と N/2 点 DCT-IV に分解 |
| N 点 DCT-IV | N-2 回の加算と N/2 回の複素数乗算により二組の N/2 点 DCT-III に分解 |
この表から,長さ N の DCT を単純に半分の長さに分解したとき,別の型の 変換が混ざり,通常のDFT のように自分自身の変換には戻ってくれません. しかし,自分自身の変換に戻らなくても,この分解は繰り返すことができて, 四つのタイプのすべてが高速に計算できます.