離散 Hartley 変換は,通常の DFT と同様に Cooley-Tukey 型の FFT の 考えが適用できます.離散 Hartley 変換 :
N-1
A = Σ a cas(2πjk/N) , cas(x) = cos(x) + sin(x)
k j=0 j
に対する周波数間引きの基数 2 の分解は次のようになります.
N/2-1
A = Σ r cas(2πjk/(N/2))
2k j=0 j
N/2-1
A = Σ s cas(2πjk/(N/2))
2k+1 j=0 j
r = a + a
j j N/2+j
s = (a − a )cos(2πj/N) + (a − a )sin(2πj/N)
j j N/2+j N/2-j N-j
通常の DFT の分解と比較すると,奇数の項の分解が少し複雑になり, a_N/2-j と a_N-j という余計な項が入ってきます.したがって,データの 上書きをする場合は,r_j と r_N/2-j と s_j と s_N/2-j の四つの項を 同時に演算する必要があります.このとき,s_j と s_N/2-j の計算で 複素数乗算に相当する演算が含まれ,通常の複素 FFT のバタフライ演算と 同じ構造になってしまいます.この変更を行った高速 Hartley 変換 (FHT) の ルーチンは次のようになります.
| リスト2.4.2-1. 周波数間引き基数 2 の FHT |
|---|
/*
離散 Hartley 変換 :
F[k]=Σ_j=0^n-1 a[j]*(cos(2*pi*j*k/n)+sin(2*pi*j*k/n)),0<=k<n
を計算する. n はデータ数で 2 の整数乗.
*/
#include <math.h>
void fht(int n, double a[])
{
int m, mh, mq, i, j, jr, ji, k, kr, ki;
double theta, wr, wi, xr, xi;
theta = 8 * atan(1.0) / n;
for (m = n; (mh = m >> 1) >= 1; m = mh) {
mq = mh >> 1;
for (i = 0; i <= mq; i++) {
/* ---- (cos + sin) == 1 ---- */
if (i == 0 || i == mq) {
for (jr = i; jr < n; jr += m) {
kr = jr + mh;
xr = a[jr] - a[kr];
a[jr] += a[kr];
a[kr] = xr;
}
continue;
}
/* ---- (cos + sin) != 1 ---- */
wr = cos(theta * i);
wi = sin(theta * i);
for (j = 0; j < n; j += m) {
jr = i + j;
ji = mh - i + j;
kr = jr + mh;
ki = ji + mh;
xr = a[jr] - a[kr];
xi = a[ji] - a[ki];
a[jr] += a[kr];
a[ji] += a[ki];
a[kr] = wr * xr + wi * xi;
a[ki] = wi * xr - wr * xi;
}
}
theta *= 2;
}
/* ---- unscrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
xr = a[j];
a[j] = a[i];
a[i] = xr;
}
}
}
|
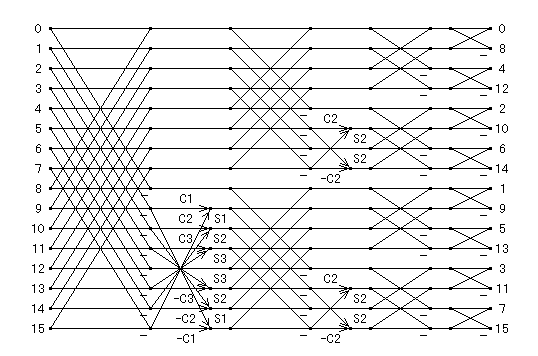
このルーチンは 2 バタフライルーチンで,cas(x) = 1 のときの例外処理を 行っています.このルーチンのフローグラフは次のようになります.
 |
| 図2.4.2-1. 周波数間引き基数 2 の FHT |
|---|
この FHT のルーチンから通常の DFT が簡単に計算できます.FHT から 通常の実数の DFT に変換するルーチンを示しておきます.
| リスト2.4.2-2. FHT を間接的に用いる実数 FFT |
|---|
/*
実数データの DFT :
F[k]=Σ_j=0^n-1 a[j]*exp(-2*pi*i*j*k/n),0<=k<n を計算する.
出力 a[0...n/2], a[n/2+1...n-1] はそれぞれ F[0...n/2] の実部,
F[n/2+1...n-1] の虚部に相当する.
*/
void rfft(int n, double a[])
{
void fht(int n, double a[]);
int nh, j;
double x;
fht(n, a);
nh = n / 2;
for (j = 1; j < nh; j++) {
x = 0.5 * (a[j] - a[n - j]);
a[j] -= x;
a[n - j] = x;
}
}
/*
実数データの DFT の逆変換:
F[k] = (a[0]+a[n/2]*(-1)^k)/2 + Σ_j=1^n/2-1 a[j]*cos(2*pi*j*k/n)
+ Σ_j=1^n/2-1 a[n-j]*sin(2*pi*j*k/n)
を計算する.
注意: スケーリングは 2/n しなければいけない.
*/
void irfft(int n, double a[])
{
void fht(int n, double a[]);
int nh, j;
double x;
nh = n / 2;
a[0] *= 0.5;
a[nh] *= 0.5;
for (j = 1; j < nh; j++) {
x = 0.5 * (a[j] - a[n - j]);
a[j] -= x;
a[n - j] = x;
}
fht(n, a);
}
|
また,複素 DFT も同様に FHT から計算できます.
次に,FHT の基数について考えます.通常の FFT と同様に,FHT も, 混合基数や大きい基数, さらに Split-Radix にすることができて,通常のFFT と同じ割合で演算量を削減できます. 次に,Split-Radix による FHT のルーチンを示します.
| リスト2.4.2-3. Split-Radix FHT |
|---|
/*
離散 Hartley 変換 :
F[k]=Σ_j=0^n-1 a[j]*(cos(2*pi*j*k/n)+sin(2*pi*j*k/n)),0<=k<n
を計算する. n はデータ数で 2 の整数乗.
*/
#include <math.h>
void fht(int n, double a[])
{
int m, mq, mqh, i, j, k;
int j0r, j0i, j1r, j1i, j2r, j2i, j3r, j3i;
double theta, w1r, w1i, w3r, w3i, x0r, x0i, x1r, x1i, x3r, x3i;
/* ---- L shaped butterflies ---- */
theta = 8 * atan(1.0) / n;
for (m = n; m > 4; m >>= 1) {
mq = m >> 2;
mqh = mq >> 1;
/* ---- (cos + sin) == sqrt(2) ---- */
w1r = 2 * cos(theta * mqh);
for (k = m; k <= n; k <<= 2) {
for (j0r = k - m; j0r < n; j0r += 2 * k) {
j1r = j0r + mqh;
j0i = j0r + mq;
j1i = j1r + mq;
j2r = j0i + mq;
j3r = j1i + mq;
j2i = j2r + mq;
j3i = j3r + mq;
x1r = a[j0r] - a[j2r];
x1i = a[j0i] - a[j2i];
a[j0r] += a[j2r];
a[j0i] += a[j2i];
a[j2r] = x1r + x1i;
a[j2i] = x1r - x1i;
x3r = w1r * (a[j1r] - a[j3r]);
x3i = w1r * (a[j1i] - a[j3i]);
a[j1r] += a[j3r];
a[j1i] += a[j3i];
a[j3r] = x3r;
a[j3i] = x3i;
}
}
for (i = 1; i < mqh; i++) {
/* ---- (cos + sin) != sqrt(2) ---- */
w1r = cos(theta * i);
w1i = sin(theta * i);
w3r = cos(theta * 3 * i);
w3i = sin(theta * 3 * i);
for (k = m; k <= n; k <<= 2) {
for (j = k - m; j < n; j += 2 * k) {
j0r = i + j;
j1r = mq - i + j;
j0i = j1r + mq;
j1i = j0r + mq;
j2r = j1i + mq;
j3r = j0i + mq;
j2i = j3r + mq;
j3i = j2r + mq;
x1r = a[j0r] - a[j2r];
x1i = a[j0i] - a[j2i];
a[j0r] += a[j2r];
a[j0i] += a[j2i];
x3r = a[j1r] - a[j3r];
x3i = a[j1i] - a[j3i];
a[j1r] += a[j3r];
a[j1i] += a[j3i];
x0r = x1r + x3r;
x0i = x1i - x3i;
a[j2r] = w1r * x0r + w1i * x0i;
a[j3r] = w1i * x0r - w1r * x0i;
x0r = x1r - x3r;
x0i = x1i + x3i;
a[j3i] = w3r * x0r + w3i * x0i;
a[j2i] = w3i * x0r - w3r * x0i;
}
}
}
theta *= 2;
}
/* ---- radix 2 butterflies (m == 4) ---- */
for (k = 4; k <= n; k <<= 2) {
for (j = k - 4; j < n; j += 2 * k) {
x0r = a[j] - a[j + 2];
x0i = a[j + 1] - a[j + 3];
a[j] += a[j + 2];
a[j + 1] += a[j + 3];
a[j + 2] = x0r;
a[j + 3] = x0i;
}
}
/* ---- radix 2 butterflies (last stage) ---- */
if (n > 1) {
for (j = 0; j < n; j += 2) {
x0r = a[j] - a[j + 1];
a[j] += a[j + 1];
a[j + 1] = x0r;
}
}
/* ---- unscrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
x0r = a[j];
a[j] = a[i];
a[i] = x0r;
}
}
}
|
このルーチンは,log(N) 段ある演算で,Split-Radix が意味を持たなくなった 時点で,基数 2 に切り替えています.したがって,通常の FFT に比べて, 切り替えを一段だけ早くしてあります.また,このルーチンは 2 バタフライの Split-Radix FFT で凝ったことは何もしていないのですが,不要な乗算は すべて取り除かれています.
次に,FHT の演算量と通常の FFT の演算量とを比較してみます.上の Split-Radix FHT のルーチンの乗算回数 μ と加算回数 α は次のように なります.
2 19 1 log N
μ = --- N log N - ---- N + 3 + --- (-1)
3 9 9
4 8 1 log N
α = --- N log N - --- N + 1 - --- (-1)
3 9 9
また,複素数乗算に相当する演算を 3 回の実数乗算と 3 回の実数加算で 計算すれば
1 3
μ = --- N log N - --- N + 2
2 2
3 3
α = --- N log N - --- N + 2
2 2
となります.これと通常の複素 Split-Radix FFT の演算量とを比較すると 演算量はちょうど半分になります.しかし,複素 DFT が二回の FHT で 計算できることを考慮すると,演算量はまったく同じということになります. さらに,FHT を DFT に変換するときの加減算も考慮すると,かえって不利に なります.しかし,FHT は複素 FFT に比べて少ないバタフライ数で済むため, 実際の計算では高速になるかもしれません.FHT は複素 FFT に比べて高速だと よく言われるようですが,FHT と FFT の比較を実際にインプリメントする ことで調べた文献[参考文献] によるとその差はほとんどないようです.