Motion of a scalar charge

5.1 Motion of a scalar charge

5.1.1 Dynamics of a point scalar charge

A point particle carries a scalar charge $q$ and moves on a world line $γ$ described by relations $zμ(λ )$ , in which $λ$ is an arbitrary parameter. The particle generates a scalar potential $Φ (x )$ and a field $Φ α(x) ≡ ∇ αΦ (x)$ . The dynamics of the entire system is governed by the action

where $Sfield$ is an action functional for a free scalar field in a spacetime with metric $gαβ$ , $Sparticle$ is the action of a free particle moving on a world line $γ$ in this spacetime, and $Sinteraction$ is an interaction term that couples the field to the particle.

The field action is given by

where the integration is over all of spacetime; the field is coupled to the Ricci scalar $R$ by an arbitrary constant $ξ$ . The particle action is

where $m0$ is the bare mass of the particle and $∘ ------------- dτ = − gμν(z)˙zμz˙ν dλ$ is the differential of proper time along the world line; we use an overdot on $zμ(λ )$ to indicate differentiation with respect to the parameter $λ$ . Finally, the interaction term is given by

Notice that both $Sparticle$ and $Sinteraction$ are invariant under a reparameterization $′ λ → λ (λ )$ of the world line.

Demanding that the total action be stationary under a variation $δΦ (x)$ of the field configuration yields the wave equation

for the scalar potential, with a charge density $μ(x)$ defined by

These equations determine the field $Φ (x ) α$ once the motion of the scalar charge is specified. On the other hand, demanding that the total action be stationary under a variation $μ δz (λ)$ of the world line yields the equations of motion for the scalar charge,

We have here adopted $τ$ as the parameter on the world line, and introduced the four-velocity $u μ(τ ) ≡ dzμ∕dτ$ . The dynamical mass that appears in Equation (387

) is defined by $m (τ) = m0 − qΦ (z )$ , which can also be written in differential form as

It should be clear that Equations (387

) and (388

) are valid only in a formal sense, because the scalar potential obtained from Equations (385

) and (386

) diverges on the world line. Before we can make sense of these equations we have to analyze the field’s singularity structure near the world line.

5.1.2 Retarded potential near the world line

The retarded solution to Equation (385 ) is $∫ √ -- Φ (x) = G+ (x,x′)μ(x′) g ′d4x ′$ , where $G+ (x, x′)$ is the retarded Green’s function introduced in Section 4.3. After substitution of Equation (386 ) we obtain

in which $z(τ)$ gives the description of the world line $γ$ . Because the retarded Green’s function is defined globally in the entire spacetime, Equation (389

) applies to any field point $x$ .

Figure 9:

The region within the dashed boundary represents the normal convex neighbourhood of the point $x$ . The world line $γ$ enters the neighbourhood at proper time $τ<$ and exits at proper time $τ>$ . Also shown are the retarded point $z (u)$ and the advanced point $z (v )$ .

We now specialize Equation (389 ) to a point $x$ near the world line (see Figure 9 ). We let $𝒩 (x)$ be the normal convex neighbourhood of this point, and we assume that the world line traverses $𝒩 (x)$ . Let $τ <$ be the value of the proper-time parameter at which $γ$ enters $𝒩 (x)$ from the past, and let $τ >$ be its value when the world line leaves $𝒩 (x)$ . Then Equation (389 ) can be broken down into the three integrals

∫ τ< ∫ τ> ∫ ∞ Φ (x ) = q G (x,z)dτ + q G (x, z)dτ + q G (x,z)d τ. − ∞ + τ< + τ> +

The third integration vanishes because $x$ is then in the past of $z(τ)$ , and $G+ (x,z) = 0$ . For the second integration, $x$ is the normal convex neighbourhood of $z(τ)$ , and the retarded Green’s function can be expressed in the Hadamard form produced in Section 4.3.2. This gives

∫ τ ∫ τ ∫ τ > > > τ G+ (x,z )dτ = τ U (x, z)δ+(σ)d τ + τ V (x,z)θ+ (− σ )dτ, < < <

and to evaluate this we refer back to Section 3.3 and let $′ x ≡ z(u)$ be the retarded point associated with $x$ ; these points are related by $σ(x,x ′) = 0$ and $′ r ≡ σα′uα$ is the retarded distance between $x$ and the world line. We resume the index convention of Section 3.3: To tensors at $x$ we assign indices $α$ , $β$ , etc.; to tensors at $x′$ we assign indices $α′$ , $β ′$ , etc.; and to tensors at a generic point $z(τ )$ on the world line we assign indices $μ$ , $ν$ , etc.

To perform the first integration we change variables from $τ$ to $σ$ , noticing that $σ$ increases as $z (τ)$ passes through $x′$ . The change of $σ$ on the world line is given by $μ dσ ≡ σ(x,z + dz ) − σ (x, z) = σμu dτ$ , and we find that the first integral evaluates to $μ U (x,z )∕(σ μu )$ with $z$ identified with $′ x$ . The second integration is cut off at $τ = u$ by the step function, and we obtain our final expression for the retarded potential of a point scalar charge:

This expression applies to a point $x$ sufficiently close to the world line that there exists a nonempty intersection between $𝒩 (x)$ and $γ$ .

5.1.3 Field of a scalar charge in retarded coordinates

When we differentiate the potential of Equation (390 ) we must keep in mind that a variation in $x$ induces a variation in $x′$ because the new points $x + δx$ and $x′ + δx ′$ must also be linked by a null geodesic – you may refer back to Section 3.3.2 for a detailed discussion. This means, for example, that the total variation of $U (x,x′)$ is $δU = U(x + δx, x′ + δx ′) − U (x, x′) = U δxα + U ′u α′ δu ;α ;α$ . The gradient of the scalar potential is therefore given by

where the “tail integral” is defined by

∫ ∫ tail u τ< Φ α (x ) = q ∇ αV (x,z )dτ + q ∇ αG+ (x,z) dτ ∫τ<− −∞ u = q ∇αG+ (x,z)dτ. (392 ) −∞

In the second form of the definition we integrate $∇ αG+ (x,z )$ from $τ = − ∞$ to almost $τ = u$ , but we cut the integration short at $τ = u− ≡ u − 0+$ to avoid the singular behaviour of the retarded Green’s function at $σ = 0$ . This limiting procedure gives rise to the first form of the definition, with the advantage that the integral need not be broken down into contributions that refer to $𝒩 (x )$ and its complement, respectively.

We shall now expand $Φ α(x)$ in powers of $r$ , and express the results in terms of the retarded coordinates $(u,r,Ωa )$ introduced in Section 3.3. It will be convenient to decompose $Φ (x) α$ in the tetrad $(eα,eα ) 0 a$ that is obtained by parallel transport of $(uα′,eα′) a$ on the null geodesic that links $x$ to $′ x ≡ z(u)$ ; this construction is detailed in Section 3.3. Note that throughout this section we set $ωab = 0$ , where $ωab$ is the rotation tensor defined by Equation (138 ): The tetrad vectors $eαa′$ are taken to be Fermi–Walker transported on $γ$ . The expansion relies on Equation (166 ) for $∂αu$ , Equation (168 ) for $∂αr$ , and we shall need

which follows from Equation (275

) and the relation $′ ′ ′ σα = − r(uα + Ωae αa )$ first encountered in Equation (144

); recall that

′ ′ ′ ′ ′ ′ R00 (u) = R α′β′uα uβ, R0a(u ) = R α′β′u αeβa , Rab (u) = Rα′β′eαa eβb

are frame components of the Ricci tensor evaluated at $x ′$ . We shall also need the expansions

and

which follow from Equations (276

); recall from Equation (141

) that the parallel propagator can be expressed as $gα′ = uα′e0 + eα′ea α α a α$ . And finally, we shall need

a relation that was first established in Equation (278

); here $R ≡ R (u)$ is the Ricci scalar evaluated at $x ′$ .

Collecting all these results gives

Φ (u, r,Ωa ) ≡ Φ (x)eα(x) 0 α 0 = qaa Ωa + 1qRa0b0 ΩaΩb + -1-(1 − 6ξ) qR + Φtail+ 𝒪 (r), (397 ) r 2 12 0 Φa(u, r,Ωa ) ≡ Φ α(x)eαa(x) q q 1 1 ( ) = − -2Ωa − -abΩbΩa − -qRb0c0Ωb ΩcΩa − -q Ra0b0Ωb − Rab0cΩbΩc r [ r 3 ] 6 ( ) + 1-q R00 − RbcΩbΩc − (1 − 6ξ)R Ωa + 1q Ra0 + RabΩb + Φtail+ 𝒪 (r), (398 ) 12 6 a

where $aa = aα′eα′ a$ are the frame components of the acceleration vector,

′ ′ Ra0b0(u) = Rα′γ′β′δ′eαa′uγ′eβb u δ′, Rab0c(u ) = R α′γ′β′δ′eαa′eγb u β′eδc′

are frame components of the Riemann tensor evaluated at $′ x$ , and

are the frame components of the tail integral evaluated at $′ x$ . Equations (397

) and (398

) show clearly that $Φ α(x)$ is singular on the world line: The field diverges as $−2 r$ when $r → 0$ , and many of the terms that stay bounded in the limit depend on $Ωa$ and therefore possess a directional ambiguity at $r = 0$ .

5.1.4 Field of a scalar charge in Fermi normal coordinates

The gradient of the scalar potential can also be expressed in the Fermi normal coordinates of Section 3.2. To effect this translation we make $¯x ≡ z(t)$ the new reference point on the world line. We resume here the notation of Section 3.4 and assign indices $¯α$ , $¯β$ , …to tensors at $¯x$ . The Fermi normal coordinates are denoted $a (t,s,ω )$ , and we let $α α (¯e0,¯ea)$ be the tetrad at $x$ that is obtained by parallel transport of $α¯ ¯α (u ,ea)$ on the spacelike geodesic that links $x$ to $¯x$ .

Our first task is to decompose $Φα (x )$ in the tetrad $(¯eα0,¯eαa)$ , thereby defining $¯Φ0 ≡ Φ α¯eα0$ and $¯Φ ≡ Φ ¯eα a α a$ . For this purpose we use Equations (224 , 225 ) and (397 , 398 ) to obtain

[ ] [ 2] ( b) a 1 2 a 1 2 a b 3 Φ¯0 = 1 + 𝒪 (r ) Φ0 + r 1 − abΩ a + 2-r ˙a + 2r R 0b0Ω + 𝒪 (r ) Φa = − 1qa˙Ωa + -1(1 − 6ξ)qR + ¯Φtail+ 𝒪 (r) 2 a 12 0

and

[ ] b 1 2 b 1 2 b c 3 [ 2 ] ¯Φa = δ a + -r a aa − -r R a0cΩ + 𝒪 (r ) Φb + raa + 𝒪 (r ) Φ0 2 2 = − q-Ω − q-a ΩbΩ + 1qa Ωba − 1qR ΩbΩc Ω − 1-qR Ωb − 1qR Ωb Ωc r2 a r b a 2 b a 3 b0c0 a 6 a0b0 3 ab0c 1 [ b c ] 1 ( b) tail + 12-q R00 − Rbc Ω Ω − (1 − 6ξ)R Ωa + 6q Ra0 + RabΩ + Φ¯a + 𝒪 (r),

where all frame components are still evaluated at $x′$ , except for $¯Φtail 0$ and $¯Φtail a$ which are evaluated at $¯x$ .

We must still translate these results into the Fermi normal coordinates $a (t,s,ω )$ . For this we involve Equations (221 , 222 , 223 ), from which we deduce, for example,

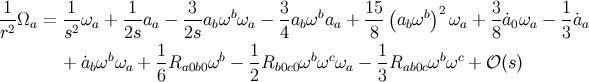
1- 1- -1- 3-- b 3- b 15( b)2 3- 1- r2Ωa = s2ωa + 2s aa − 2sabω ωa − 4abω aa + 8 abω ωa + 8 ˙a0ωa − 3 ˙aa b 1 b 1 b c 1 b c + ˙abω ωa + -Ra0b0ω − --Rb0c0ω ω ωa − --Rab0cω ω + 𝒪 (s ) 6 2 3

and

1 1 1 3 ( )2 1 --abΩbΩa = -abωbωa + -abωbaa − -- abωb ωa − -a˙0 ωa − ˙abωbωa + 𝒪 (s), r s 2 2 2

in which all frame components (on the right-hand side of these relations) are now evaluated at $x¯$ ; to obtain the second relation we expressed $aa(u)$ as $aa(t) − sa˙a (t) + 𝒪 (s2)$ , since according to Equation (221 ), $u = t − s + 𝒪(s2)$ .

Collecting these results yields

Φ¯ (t,s,ωa) ≡ Φ (x)¯eα(x) 0 α 0 = − 1qa˙ ωa + -1(1 − 6ξ)qR + ¯Φtail+ 𝒪 (s ), (400 ) 2 a 12 0 Φ¯a (t,s,ωa) ≡ Φ α(x)¯eαa(x) q q ( ) 3 3 ( ) 1 1 = − --ωa − ---aa − abωb ωa + -qabωbaa − -q abωb 2ωa + -q˙a0ωa + --q˙aa s2 2s 4 8 8 3 − 1qR ωb + 1-qR ωbωcω + -1-q[R − R ωbωc − (1 − 6ξ)R ]ω 3 a0b0 6 b0c0 a 12 00 bc a 1 ( b) tail + 6q Ra0 + Rabω + ¯Φ a + 𝒪 (s). (401 )

In these expressions, $¯α aa(t) = a¯αea$ are the frame components of the acceleration vector evaluated at $¯x$ , $˙a0(t) = ˙a¯αu¯α$ and $˙aa(t) = a˙¯αe¯αa$ are frame components of its covariant derivative, $R (t) = R ¯¯eα¯u ¯γe¯βu¯δ a0b0 α¯¯γβδ a b$ are frame components of the Riemann tensor evaluated at $¯x$ ,

R00 (t) = R ¯α¯βu¯αu ¯β, R0a (t) = R ¯α¯βuα¯e ¯βa, Rab(t) = R ¯α¯βe¯αae¯β b

are frame components of the Ricci tensor, and $R (t)$ is the Ricci scalar evaluated at $¯x$ . Finally, we have that

are the frame components of the tail integral – see Equation (392

) – evaluated at $¯x ≡ z(t)$ .

We shall now compute the averages of $¯ Φ0$ and $¯ Φa$ over $S (t,s)$ , a two-surface of constant $t$ and $s$ ; these will represent the mean value of the field at a fixed proper distance away from the world line, as measured in a reference frame that is momentarily comoving with the particle. The two-surface is charted by angles $θA$ ( $A = 1,2$ ) and it is described, in the Fermi normal coordinates, by the parametric relations $a a A xˆ = sω (θ )$ ; a canonical choice of parameterization is $ωa = (sinθ cosφ,sin θsinφ, cosθ)$ . Introducing the transformation matrices $ωa ≡ ∂ωa ∕∂θA A$ , we find from Equation (127 ) that the induced metric on $S(t,s)$ is given by

where $a b ωAB ≡ δabω AωB$ is the metric of the unit two-sphere, and where $a c b d RAB ≡ RacbdωAω ωBω$ depends on $t$ and the angles $A θ$ . From this we infer that the element of surface area is given by

where $∘ --------- dΩ = det[ωAB ]d2θ$ is an element of solid angle – in the canonical parameterization, $dΩ = sinθ dθdφ$ . Integration of Equation (404

) produces the total surface area of $S(t,s)$ , and $𝒜 = 4πs2 [1 − -1s2Rab + 𝒪 (s3)] 18 ab$ .

The averaged fields are defined by

where the quantities to be integrated are scalar functions of the Fermi normal coordinates. The results

are easy to establish, and we obtain

⟨¯ ⟩ 1-- ¯tail Φ0 = 12(1 − 6ξ)qR + Φ0 + 𝒪(s), (407 ) ⟨ ⟩ q 1 1 ¯Φa = − --aa + -q ˙aa + -qRa0 + Φ¯taail+ 𝒪 (s). (408 ) 3s 3 6

The averaged field is still singular on the world line. Regardless, we shall take the formal limit $s → 0$ of the expressions displayed in Equations (407

) and (408

). In the limit the tetrad $(¯eα0,¯eαa)$ reduces to $(u¯α,eα¯) a$ , and we can reconstruct the field at $¯x$ by invoking the completeness relations $¯α ¯α α¯ a δ ¯β = − u u ¯β + ea e¯β$ . We thus obtain

where the tail integral can be copied from Equation (392

The tensors appearing in Equation (409

) all refer to $¯x ≡ z (t)$ , which now stands for an arbitrary point on the world line $γ$ .

5.1.5 Singular and radiative fields

The singular potential

is the (unphysical) solution to Equations (385

) and (386

) that is obtained by adopting the singular Green’s function of Equation (295

) instead of the retarded Green’s function. As we shall see, the resulting singular field $ΦS(x ) α$ reproduces the singular behaviour of the retarded solution; the difference, $R S Φ α(x) = Φ α(x) − Φα(x )$ , is smooth on the world line.

To evaluate the integral of Equation (411 ) we assume once more that $x$ is sufficiently close to $γ$ that the world line traverses $𝒩 (x)$ (refer back to Figure 9 ). As before we let $τ<$ and $τ>$ be the values of the proper-time parameter at which $γ$ enters and leaves $𝒩 (x)$ , respectively. Then Equation (411 ) can be broken down into the three integrals,

∫ τ< ∫ τ> ∫ ∞ ΦS (x ) = q GS(x,z )dτ + q GS (x,z)dτ + q GS (x,z)d τ. − ∞ τ< τ>

The first integration vanishes because $x$ is then in the chronological future of $z(τ)$ , and $GS (x,z) = 0$ by Equation (286 ). Similarly, the third integration vanishes because $x$ is then in the chronological past of $z(τ)$ . For the second integration, $x$ is the normal convex neighbourhood of $z(τ)$ , the singular Green’s function can be expressed in the Hadamard form of Equation (297 ), and we have

∫ τ> ∫ τ> ∫ τ> ∫ τ> 1- 1- 1- τ<GS (x,z) dτ = 2 τ<U (x,z)δ+ (σ)dτ + 2 τ< U (x, z)δ− (σ) dτ − 2 τ<V (x,z)θ(σ) dτ.

To evaluate these we re-introduce the retarded point $x′ ≡ z(u)$ and let $x′′ ≡ z(v)$ be the advanced point associated with $x$ ; we recall from Section 3.4.4 that these points are related by $′′ σ (x, x ) = 0$ and that $α′′ radv ≡ − σα′′u$ is the advanced distance between $x$ and the world line.

To perform the first integration we change variables from $τ$ to $σ$ , noticing that $σ$ increases as $z(τ)$ passes through $x′$ ; the integral evaluates to $U (x,x ′)∕r$ . We do the same for the second integration, but we notice now that $σ$ decreases as $z(τ )$ passes through $′′ x$ ; the integral evaluates to $U (x,x′′)∕radv$ . The third integration is restricted to the interval $u ≤ τ ≤ v$ by the step function, and we obtain our final expression for the singular potential of a point scalar charge:

We observe that $ΦS(x )$ depends on the state of motion of the scalar charge between the retarded time $u$ and the advanced time $v$ ; contrary to what was found in Section 5.1.2 for the retarded potential, there is no dependence on the particle’s remote past.

We use the techniques of Section 5.1.3 to differentiate the potential of Equation (412 ). We find

ΦS (x) = − -q-U (x,x ′)∂αr − ---q--U (x,x ′′)∂ αradv + -q-U;α(x,x′) + q-U;α′(x,x′)uα′∂αu α 2r2 2radv2 2r 2r --q-- ′′ --q-- ′′ α′′ 1- ′ 1- ′′ + 2r U;α(x,x ) + 2r U;α′′(x,x )u ∂αv + 2 qV (x, x)∂ αu − 2qV (x,x )∂ αv ad∫vv adv − 1q ∇ αV (x,z)d τ, (413 ) 2 u

and we would like to express this as an expansion in powers of $r$ . For this we shall rely on results already established in Section 5.1.3, as well as additional expansions that will involve the advanced point $′′ x$ . Those we develop now.

We recall first that a relation between retarded and advanced times was worked out in Equation (229 ), that an expression for the advanced distance was displayed in Equation (230 ), and that Equations (231 ) and (232 ) give expansions for $∂αv$ and $∂αradv$ , respectively.

To derive an expansion for $U (x,x ′′)$ we follow the general method of Section 3.4.4 and define a function $U (τ) ≡ U (x, z(τ))$ of the proper-time parameter on $γ$ . We have that

′′ ′ ˙ ′ 1-¨ ′2 ( ′3) U (x,x ) ≡ U (v) = U (u + Δ ) = U(u ) + U (u)Δ + 2U (u)Δ + O Δ ,

where overdots indicate differentiation with respect to $τ$ , and where $Δ′ ≡ v − u$ . The leading term $′ U (u) ≡ U (x,x )$ was worked out in Equation (393 ), and the derivatives of $U (τ)$ are given by

1 U˙(u) = U;α′uα′ = − -r (R00 + R0aΩa ) + 𝒪 (r2) 6

and

1 ¨U(u ) = U;α′β′uα′u β′ + U;α′aα′ =-R00 + 𝒪 (r), 6

according to Equations (395 ) and (276 ). Combining these results together with Equation (229 ) for $Δ ′$ gives

which should be compared with Equation (393

). It should be emphasized that in Equation (414

) and all equations below, the frame components of the Ricci tensor are evaluated at the retarded point $′ x ≡ z(u)$ , and not at the advanced point. The preceding computation gives us also an expansion for $′′ U;α′′u α ≡ ˙U(v) = U˙(u) + ¨U (u)Δ′ + 𝒪(Δ ′2)$ . This becomes

which should be compared with Equation (395

We proceed similarly to derive an expansion for $′′ U;α(x, x )$ . Here we introduce the functions $U α(τ) ≡ U;α(x,z(τ))$ and express $′′ U;α(x,x )$ as $˙ ′ ′2 U α(v) = Uα(u ) + U α(u)Δ + 𝒪 (Δ )$ . The leading term $U α(u) ≡ U;α(x,x′)$ was computed in Equation (394 ), and

U˙α(u) = U;αβ′u β′ = − 1-gαα′R α′0 + 𝒪 (r) 6

follows from Equation (276 ). Combining these results together with Equation (229 ) for $Δ ′$ gives

and this should be compared with Equation (394

The last expansion we shall need is

which follows at once from Equation (396

) and the fact that $V (x,x′′) − V (x,x′) = 𝒪 (r)$ ; the Ricci scalar is evaluated at the retarded point $x′$ .

It is now a straightforward (but tedious) matter to substitute these expansions (all of them!) into Equation (413 ) and obtain the projections of the singular field $S Φ α(x)$ in the same tetrad $α α (e0,ea)$ that was employed in Section 5.1.3. This gives

S a S α Φ0(u, r,Ω ) ≡ Φ α(x)e0(x) q- a 1- a b = r aaΩ + 2 qRa0b0Ω Ω + 𝒪 (r), (418 ) ΦS(u, r,Ωa) ≡ ΦS (x)eα(x) a α a = − q-Ω − qa Ωb Ω − 1q ˙a − 1qR ΩbΩc Ω − 1-q(R Ωb − R Ωb Ωc) r2 a r b a 3 a 3 b0c0 a 6 a0b0 ab0c 1-- [ b c ] 1- b + 12q R00 − RbcΩ Ω − (1 − 6ξ )R Ωa + 6qRab Ω , (419 )

in which all frame components are evaluated at the retarded point $′ x ≡ z(u)$ . Comparison of these expressions with Equations (397

) and (398

) reveals that the retarded and singular fields share the same singularity structure.

The difference between the retarded field of Equations (397 , 398 ) and the singular field of Equations (418 , 419 ) defines the radiative field $R Φ α(x)$ . Its tetrad components are

R 1 tail Φ 0 = ---(1 − 6ξ)qR + Φ 0 + 𝒪 (r), (420 ) 12 ΦRa = 1-q˙aa + 1qRa0 + Φtaail+ 𝒪 (r), (421 ) 3 6

and we see that $ΦRα(x)$ is a smooth vector field on the world line. There is therefore no obstacle in evaluating the radiative field directly at $x = x ′$ , where the tetrad $(eα,eα) 0 a$ becomes $(uα′,e α′) a$ . Reconstructing the field at $′ x$ from its frame components, we obtain

where the tail term can be copied from Equation (392

The tensors appearing in Equation (422

) all refer to the retarded point $x′ ≡ z(u)$ , which now stands for an arbitrary point on the world line $γ$ .

5.1.6 Equations of motion

The retarded field $Φα(x)$ of a point scalar charge is singular on the world line, and this behaviour makes it difficult to understand how the field is supposed to act on the particle and affect its motion. The field’s singularity structure was analyzed in Sections 5.1.3 and 5.1.4, and in Section 5.1.5 it was shown to originate from the singular field $ΦSα(x)$ ; the radiative field $ΦRα(x) = Φ α(x) − ΦSα(x )$ was then shown to be smooth on the world line.

To make sense of the retarded field’s action on the particle we temporarily model the scalar charge not as a point particle, but as a small hollow shell that appears spherical when observed in a reference frame that is momentarily comoving with the particle; the shell’s radius is $s0$ in Fermi normal coordinates, and it is independent of the angles contained in the unit vector $ωa$ . The net force acting at proper time $τ$ on this hollow shell is the average of $qΦ (τ,s ,ωa ) α 0$ over the surface of the shell. This was worked out at the end of Section 5.1.4, and ignoring terms that disappear in the limit $s0 → 0$ , we obtain

where

is formally a divergent quantity and

is the tail part of the force; all tensors in Equation (424

) are evaluated at an arbitrary point $z(τ)$ on the world line.

Substituting Equations (424 ) and (426 ) into Equation (387 ) gives rise to the equations of motion

for the scalar charge, with $m ≡ m0 − qΦ (z)$ denoting the (also formally divergent) dynamical mass of the particle. We see that $m$ and $δm$ combine in Equation (427

) to form the particle’s observed mass $mobs$ , which is taken to be finite and to give a true measure of the particle’s inertia. All diverging quantities have thus disappeared into the process of mass renormalization. Substituting Equations (424

) and (426

) into Equation (388

), in which we replace $m$ by $mobs = m + δm$ , returns an expression for the rate of change of the observed mass,

That the observed mass is not conserved is a remarkable property of the dynamics of a scalar charge in a curved spacetime. Physically, this corresponds to the fact that in a spacetime with a time-dependent metric, a scalar charge radiates monopole waves and the radiated energy comes at the expense of the particle’s inertial mass.

Apart from the term proportional to $δm$ , the averaged field of Equation (424 ) has exactly the same form as the radiative field of Equation (422 ), which we re-express as

The force acting on the point particle can therefore be thought of as originating from the (smooth) radiative field, while the singular field simply contributes to the particle’s inertia. After mass renormalization, Equations (427

) and (428

) are equivalent to the statements

where we have dropped the superfluous label “obs” on the particle’s observed mass. Another argument in support of the claim that the motion of the particle should be affected by the radiative field only was presented in Section 4.3.5.

The equations of motion displayed in Equations (427 ) and (428 ) are third-order differential equations for the functions $μ z (τ)$ . It is well known that such a system of equations admits many unphysical solutions, such as runaway situations in which the particle’s acceleration increases exponentially with $τ$ , even in the absence of any external force [25 , 30 , 47 ]. And indeed, our equations of motion do not yet incorporate an external force which presumably is mostly responsible for the particle’s acceleration. Both defects can be cured in one stroke. We shall take the point of view, the only admissible one in a classical treatment, that a point particle is merely an idealization for an extended object whose internal structure – the details of its charge distribution – can be considered to be irrelevant. This view automatically implies that our equations are meant to provide only an approximate description of the object’s motion. It can then be shown [47 , 26 ] that within the context of this approximation, it is consistent to replace, on the right-hand side of the equations of motion, any occurrence of the acceleration vector by $μ f ext∕m$ , where $μ fext$ is the external force acting on the particle. Because $μ fext$ is a prescribed quantity, differentiation of the external force does not produce higher derivatives of the functions $z μ(τ)$ , and the equations of motion are properly of second order.

We shall therefore write, in the final analysis, the equations of motion in the form

and

where $m$ denotes the observed inertial mass of the scalar charge, and where all tensors are evaluated at $z(τ)$ . We recall that the tail integration must be cut short at $τ ′ = τ− ≡ τ − 0+$ to avoid the singular behaviour of the retarded Green’s function at coincidence; this procedure was justified at the beginning of Section 5.1.3. Equations (431

) and (432

) were first derived by Theodore C. Quinn in 2000 [48 ]. In his paper Quinn also establishes that the total work done by the scalar self-force matches the amount of energy radiated away by the particle.