Motion of an electric charge

5.2 Motion of an electric charge

5.2.1 Dynamics of a point electric charge

A point particle carries an electric charge $e$ and moves on a world line $γ$ described by relations $zμ(λ)$ , in which $λ$ is an arbitrary parameter. The particle generates a vector potential $A α(x)$ and an electromagnetic field $F αβ(x) = ∇ αAβ − ∇ βA α$ . The dynamics of the entire system is governed by the action

where $Sfield$ is an action functional for a free electromagnetic field in a spacetime with metric $gαβ$ , $Sparticle$ is the action of a free particle moving on a world line $γ$ in this spacetime, and $Sinteraction$ is an interaction term that couples the field to the particle.

The field action is given by

where the integration is over all of spacetime. The particle action is

where $m$ is the bare mass of the particle and $∘ ------------- dτ = − gμν(z)z˙μz˙ν dλ$ is the differential of proper time along the world line; we use an overdot to indicate differentiation with respect to the parameter $λ$ . Finally, the interaction term is given by

Notice that both $Sparticle$ and $Sinteraction$ are invariant under a reparameterization $λ → λ′(λ )$ of the world line.

Demanding that the total action be stationary under a variation $α δA (x)$ of the vector potential yields Maxwell’s equations

with a current density $jα(x)$ defined by

These equations determine the electromagnetic field $F αβ$ , once the motion of the electric charge is specified. On the other hand, demanding that the total action be stationary under a variation $μ δz (λ)$ of the world line yields the equations of motion for the electric charge,

We have adopted $τ$ as the parameter on the world line, and introduced the four-velocity $μ μ u (τ ) ≡ dz ∕dτ$ .

The electromagnetic field $Fαβ$ is invariant under a gauge transformation of the form $A α → A α + ∇ αΛ$ , in which $Λ(x)$ is an arbitrary scalar function. This function can always be chosen so that the vector potential satisfies the Lorenz gauge condition,

Under this condition the Maxwell equations of Equation (437

) reduce to a wave equation for the vector potential,

where $αβ □ = g ∇ α∇ β$ is the wave operator and $α R β$ is the Ricci tensor. Having adopted $τ$ as the parameter on the world line, we can re-express the current density of Equation (438

) as

and we shall use Equations (441

) and (442

) to determine the electromagnetic field of a point electric charge. The motion of the particle is in principle determined by Equation (439

), but because the vector potential obtained from Equation (441

) is singular on the world line, these equations have only formal validity. Before we can make sense of them we will have to analyze the field’s singularity structure near the world line. The calculations to be carried out parallel closely those presented in Section 5.1 for the case of a scalar charge; the details will therefore be kept to a minimum and the reader is referred to Section 5.1 for additional information.

5.2.2 Retarded potential near the world line

The retarded solution to Equation (441 ) is $∫ √ -- A α(x) = G α+β′(x, x′)jβ′(x′) g′d4x ′$ , where $G +αβ′(x,x′)$ is the retarded Green’s function introduced in Section 4.4. After substitution of Equation (442 ) we obtain

in which $zμ(τ )$ gives the description of the world line $γ$ and $u μ(τ) = dzμ∕dτ$ . Because the retarded Green’s function is defined globally in the entire spacetime, Equation (443

) applies to any field point $x$ .

We now specialize Equation (443 ) to a point $x$ close to the world line. We let $𝒩 (x )$ be the normal convex neighbourhood of this point, and we assume that the world line traverses $𝒩 (x)$ (refer back to Figure 9 ). As in Section 5.1.2 we let $τ<$ and $τ>$ be the values of the proper-time parameter at which $γ$ enters and leaves $𝒩 (x )$ , respectively. Then Equation (443 ) can be expressed as

∫ τ< ∫ τ> ∫ ∞ A α(x) = e G +αμ(x,z )u μdτ + e G +αμ(x,z )uμdτ + e G +αμ(x,z)u μdτ. −∞ τ< τ>

The third integration vanishes because $x$ is then in the past of $z(τ)$ , and $G +αμ(x,z ) = 0$ . For the second integration, $x$ is the normal convex neighbourhood of $z(τ )$ , and the retarded Green’s function can be expressed in the Hadamard form produced in Section 4.4.2. This gives

∫ τ> ∫ τ> ∫ τ> G α (x,z)uμ dτ = Uα (x,z)uμδ (σ)dτ + V α(x,z)u μθ (− σ)dτ, τ< + μ τ< μ + τ< μ +

and to evaluate this we let $′ x ≡ z(u)$ be the retarded point associated with $x$ ; these points are related by $′ σ (x,x ) = 0$ and $α′ r ≡ σα′u$ is the retarded distance between $x$ and the world line. To perform the first integration we change variables from $τ$ to $σ$ , noticing that $σ$ increases as $z(τ)$ passes through $x ′$ ; the integral evaluates to $U αβ′uβ′∕r$ . The second integration is cut off at $τ = u$ by the step function, and we obtain our final expression for the vector potential of a point electric charge:

This expression applies to a point $x$ sufficiently close to the world line that there exists a nonempty intersection between $𝒩 (x)$ and $γ$ .

5.2.3 Electromagnetic field in retarded coordinates

When we differentiate the vector potential of Equation (444 ) we must keep in mind that a variation in $x$ induces a variation in $′ x$ , because the new points $x + δx$ and $′ ′ x + δx$ must also be linked by a null geodesic. Taking this into account, we find that the gradient of the vector potential is given by

∇βA α(x) = e- β′ e- β′ e-( β′ γ′ β′) β′ tail − r2U αβ′u ∂βr + rUαβ′;βu + r U αβ′;γ′u u + Uαβ′a ∂ βu + eVαβ′u ∂βu + A αβ(x), (445 )

where the “tail integral” is defined by

∫ u ∫ τ< Ataαiβl(x) = e ∇ βV αμ(x,z)uμ dτ + e ∇ βG+ αμ(x,z)uμ dτ τ< − ∞ ∫ u− = e ∇βG+ αμ(x, z)uμ dτ. (446 ) −∞

The second form of the definition, in which we integrate the gradient of the retarded Green’s function from $τ = − ∞$ to $− + τ = u ≡ u − 0$ to avoid the singular behaviour of the retarded Green’s function at $σ = 0$ , is equivalent to the first form.

We shall now expand $Fα β = ∇ αAβ − ∇ βA α$ in powers of $r$ , and express the result in terms of the retarded coordinates $(u,r,Ωa )$ introduced in Section 3.3. It will be convenient to decompose the electromagnetic field in the tetrad $α α (e0,ea)$ that is obtained by parallel transport of $α′ α′ (u ,e a )$ on the null geodesic that links $x$ to $′ x ≡ z(u)$ ; this construction is detailed in Section 3.3. Note that throughout this section we set $ωab = 0$ , where $ωab$ is the rotation tensor defined by Equation (138 ): The tetrad vectors $eα′ a$ are taken to be Fermi–Walker transported on $γ$ . We recall from Equation (141 ) that the parallel propagator can be expressed as $gα′= uα′e0+ eα′ea α α a α$ . The expansion relies on Equation (166 ) for $∂αu$ , Equation (168 ) for $∂αr$ , and we shall need

which follows from Equation (323

) and the relation $σα′ = − r(uα′ + Ωae α′) a$ first encountered in Equation (144

). We shall also need the expansions

and

that follow from Equations (323

, 324

, 325

). And finally, we shall need

a relation that was first established in Equation (327

Collecting all these results gives

a α β Fa0(u,r,Ω ) ≡ Fαβ(x )ea (x )e0(x) -e e-( b ) 1- b c 1- ( b b c) = r2Ωa − r aa − abΩ Ωa + 3 eRb0c0Ω Ω Ωa − 6e 5Ra0b0Ω + Rab0cΩ Ω 1 ( ) 1 1 + ---e 5R00 + RbcΩbΩc + R Ωa + -eRa0 − -eRab Ωb + Fata0il+ 𝒪 (r), (451 ) 12 β 3 6 Fab(u,r,Ωa ) ≡ Fαβ(x )eαa (x )eb(x) e 1 c = --(aaΩb − Ωaab) + --e(Ra0bc − Rb0ac + Ra0c0Ωb − ΩaRb0c0 )Ω r 2 − 1-e(Ra0 Ωb − ΩaRb0 ) + F taaibl+ 𝒪 (r), (452 ) 2

where

are the frame components of the tail integral; this is obtained from Equation (446

) evaluated at $x′$ :

It should be emphasized that in Equations (451

) and (452

), all frame components are evaluated at the retarded point $x′ ≡ z(u)$ associated with $x$ ; for example, $′ aa ≡ aa(u) ≡ aα′eαa$ . It is clear from these equations that the electromagnetic field $Fαβ(x)$ is singular on the world line.

5.2.4 Electromagnetic field in Fermi normal coordinates

We now wish to express the electromagnetic field in the Fermi normal coordinates of Section 3.2; as before those will be denoted $(t,s, ωa)$ . The translation will be carried out as in Section 5.1.4, and we will decompose the field in the tetrad $(¯eα,¯eα ) 0 a$ that is obtained by parallel transport of $(u¯α,eα¯) a$ on the spacelike geodesic that links $x$ to the simultaneous point $¯x ≡ z(t)$ .

Our first task is to decompose $Fαβ(x )$ in the tetrad $(¯eα0 ,¯eαa)$ , thereby defining $β ¯Fa0 ≡ Fαβ ¯eαa¯e0$ and $¯Fab ≡ Fαβ¯eαa ¯eβb$ . For this purpose we use Equations (224 , 225 ) and (451 , 452 ) to obtain

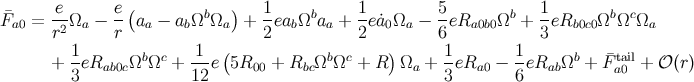
( ) F¯a0 = e-Ωa − e- aa − abΩbΩa + 1eabΩbaa + 1ea˙0Ωa − 5eRa0b0Ωb + 1eRb0c0ΩbΩc Ωa r2 r 2 2 6 3 1- b c -1- ( b c ) 1- 1- b ¯tail + 3eRab0cΩ Ω + 12e 5R00 + RbcΩ Ω + R Ωa + 3eRa0 − 6eRabΩ + F a0 + 𝒪 (r)

and

1 1 1 F¯ab = -e(Ωa ˙ab − ˙aaΩb) + -e (Ra0bc − Rb0ac)Ωc − -e (Ra0Ωb − ΩaRb0 ) + ¯Ftaabil+ 𝒪 (r), 2 2 2

where all frame components are still evaluated at $x ′$ , except for

¯F tail ≡ F tai¯l(¯x)e¯αu ¯β, F¯tail≡ F ta¯il(¯x)e¯αe¯β, a0 α¯β a ab ¯αβ a b

which are evaluated at $¯x$ .

We must still translate these results into the Fermi normal coordinates $(t,s,ωa )$ . For this we involve Equations (221 , 222 , 223 ), and we recycle some computations that were first carried out in Section 5.1.4. After some algebra, we arrive at

¯ a α β Fa0(t,s, ω ) ≡ Fαβ(x )e¯a (x)¯e0(x) -e e-( b ) 3- b 3-( b)2 3- 2- = s2ωa − 2s aa + abω ωa + 4eabω aa + 8e abω ωa + 8 e˙a0ωa + 3 e˙aa 2 1 1 ( ) − -eRa0b0ωb − --eRb0c0ωb ωcωa + ---e 5R00 + Rbc ωbωc + R ωa 3 6 12 + 1-eRa0 − 1-eRabωb + F¯tail+ 𝒪 (s), (455 ) 3 6 a0 ¯Fab(t,s, ωa) ≡ Fαβ(x )e¯α (x)¯eβ(x) a b = 1e (ωa˙ab − ˙aaωb) + 1e (Ra0bc − Rb0ac)ωc − 1e(Ra0 ωb − ωaRb0) + F¯taabil+ 𝒪 (s), 2 2 2 (456 )

where all frame components are now evaluated at $¯x ≡ z(t)$ ; for example, $¯α aa ≡ aa(t) ≡ a¯αea$ .

Our next task is to compute the averages of $F¯a0$ and $F¯ab$ over $S (t,s )$ , a two-surface of constant $t$ and $s$ . These are defined by

where $d𝒜$ is the element of surface area on $S(t,s)$ , and $∮ 𝒜 = d𝒜$ . Using the methods developed in Section 5.1.4, we find

⟨ ⟩ 2e 2 1 F¯a0 = − --aa + --e˙aa + -eRa0 + F¯taa0il+ 𝒪 (s), (458 ) ⟨ ⟩ 3s 3 3 ¯Fab = ¯Ftaabil+ 𝒪 (s). (459 )

The averaged field is singular on the world line, but we nevertheless take the formal limit $s → 0$ of the expressions displayed in Equations (458

) and (459

). In the limit the tetrad $α α (¯e0,¯ea)$ becomes $(uα¯, e¯αa)$ , and we can easily reconstruct the field at $¯x$ from its frame components. We thus obtain

where the tail term can be copied from Equation (454

The tensors appearing in Equation (460

) all refer to $¯x ≡ z (t)$ , which now stands for an arbitrary point on the world line $γ$ .

5.2.5 Singular and radiative fields

The singular vector potential

is the (unphysical) solution to Equations (441

) and (442

) that is obtained by adopting the singular Green’s function of Equation (335

) instead of the retarded Green’s function. We will see that the singular field $S F αβ$ reproduces the singular behaviour of the retarded solution, and that the difference, $F R = Fαβ − F S αβ αβ$ , is smooth on the world line.

To evaluate the integral of Equation (462 ) we assume once more that $x$ is sufficiently close to $γ$ that the world line traverses $𝒩 (x)$ (refer back to Figure 9 ). As before we let $τ<$ and $τ>$ be the values of the proper-time parameter at which $γ$ enters and leaves $𝒩 (x)$ , respectively. Then Equation (462 ) becomes

∫ ∫ ∫ α τ< α μ τ> α μ ∞ α μ AS(x) = e G Sμ(x,z )u dτ + e G Sμ(x,z )u dτ + e G Sμ(x,z)u dτ. −∞ τ< τ>

The first integration vanishes because $x$ is then in the chronological future of $z(τ)$ , and $G Sαμ(x,z) = 0$ by Equation (338 ). Similarly, the third integration vanishes because $x$ is then in the chronological past of $z(τ)$ . For the second integration, $x$ is the normal convex neighbourhood of $z(τ)$ , the singular Green’s function can be expressed in the Hadamard form of Equation (344 ), and we have

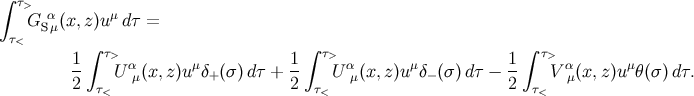
∫ τ> G Sαμ(x,z )u μdτ = τ< 1 ∫ τ> 1 ∫ τ> 1∫ τ> -- U αμ(x, z)uμδ+(σ )dτ + -- U αμ(x,z)uμδ− (σ )dτ − -- V αμ(x,z)uμθ(σ )dτ. 2 τ< 2 τ< 2 τ<

To evaluate these we let $x ′ ≡ z(u )$ and $x′′ ≡ z(v)$ be the retarded and advanced points associated with $x$ , respectively. To perform the first integration we change variables from $τ$ to $σ$ , noticing that $σ$ increases as $z(τ )$ passes through $′ x$ ; the integral evaluates to $α β′ U β′u ∕r$ . We do the same for the second integration, but we notice now that $σ$ decreases as $z(τ)$ passes through $x′′$ ; the integral evaluates to $Uαβ′′uβ′′∕radv$ , where $radv ≡ − σ α′′uα′′$ is the advanced distance between $x$ and the world line. The third integration is restricted to the interval $u ≤ τ ≤ v$ by the step function, and we obtain the expression

for the singular vector potential.

Differentiation of Equation (463 ) yields

S e β′ e β′′ e β′ ∇ βAα(x ) = − 2r2-Uαβ′u ∂βr − 2r---2U αβ′′u ∂βradv + 2rU αβ′;βu e ( ′ ′ adv ′) e ′′ + --- U αβ′;γ′u βuγ + Uαβ′aβ ∂ βu + -----Uαβ′′;βuβ 2r 2radv --e--( β′′ γ′′ β′′) 1- β′ + 2radv Uαβ′′;γ′′u u + U αβ′′a ∂ βv + 2eV αβ′u ∂βu 1 1 ∫ v − -eV αβ′′uβ′′∂βv − -e ∇ βVαμ(x,z )uμdτ, (464 ) 2 2 u

and we would like to express this as an expansion in powers of $r$ . For this we will rely on results already established in Section 5.2.3, as well as additional expansions that will involve the advanced point $′′ x$ . We recall that a relation between retarded and advanced times was worked out in Equation (229

), that an expression for the advanced distance was displayed in Equation (230

), and that Equations (231

) and (232

) give expansions for $∂αv$ and $∂αradv$ , respectively.

To derive an expansion for $β′′ U αβ′′u$ we follow the general method of Section 3.4.4 and introduce the functions $Uα (τ ) ≡ Uαμ(x,z)u μ$ . We have that

β′′ ˙ ′ 1¨ ′2 ( ′3) Uαβ′′u ≡ Uα(v) = U α(u) + Uα(u )Δ + 2Uα (u )Δ + O Δ ,

where overdots indicate differentiation with respect to $τ$ , and $Δ ′ ≡ v − u$ . The leading term $β′ U α(u) ≡ Uα β′u$ was worked out in Equation (447 ), and the derivatives of $U α(τ)$ are given by

[ ( ) ] U˙α(u) = U αβ′;γ′uβ′uγ′ + Uαβ′aβ′ = g αα′ aα′ + 1rR α′0b0Ωb − 1-r R00 + R0b Ωb u α′ + 𝒪 (r2) 2 6

and

′ ′ ′ ( ′ ′ ′ ′) ′ ′[ 1 ] ¨Uα(u ) = U αβ′;γ′δ′uβ uγu δ + Uαβ′;γ′ 2aβ uγ + uβ aγ + Uαβ′˙aβ = gαα a˙α′ +-R00u α′ + 𝒪(r) , 6

according to Equations (449 ) and (325 ). Combining these results together with Equation (229 ) for $′ Δ$ gives

[ U ′′uβ′′ = gα′ u ′ + 2r (1 − ra Ωb) a ′ + 2r2˙a ′ + r2R ′ Ωb αβ α α b α α α 0b0 1 ( ) ] + --r2 R00 − 2R0aΩa + RabΩa Ωb u α′ + 𝒪 (r3) , (465 ) 12

which should be compared with Equation (447

). It should be emphasized that in Equation (465

) and all equations below, all frame components are evaluated at the retarded point $′ x$ , and not at the advanced point. The preceding computation gives us also an expansion for

β′′ γ′′ β′′ ′ ′2 Uαβ′′;γ′′u u + Uα β′′a ≡ ˙Uα(v) = U˙α(u) + ¨Uα(u )Δ + 𝒪 (Δ ),

which becomes

[ ] U ′′ ′′uβ′′uγ′′ + U ′′aβ′′ = gα′ a ′ + 2ra˙′ + 1rR ′ Ωb + 1r(R − R Ωb) u ′ + 𝒪 (r2) , αβ ;γ αβ α α α 2 α 0b0 6 00 0b α (466 )

and which should be compared with Equation (449

We proceed similarly to derive an expansion for $U αβ′′;βu β′′$ . Here we introduce the functions $μ U αβ(τ) ≡ Uαμ;βu$ and express $′′ β′′ U αβ ;βu$ as $˙ ′ ′2 U αβ(v) = Uαβ(u ) + U αβ(u)Δ + 𝒪 (Δ )$ . The leading term $β′ U αβ(u) ≡ Uα β′;βu$ was computed in Equation (448 ), and

′ ′ ′ 1 ′ ′[ 1 ] ˙Uαβ(u) = U αβ′;βγ′u βuγ + Uαβ′;βa β = --gααgββ R α′0β′0 − -uα′R β′0 + 𝒪 (r) 2 3

follows from Equation (324 ). Combining these results together with Equation (229 ) for $Δ ′$ gives

and this should be compared with Equation (448

). The last expansion we shall need is

which follows at once from Equation (450

It is now a straightforward (but still tedious) matter to substitute these expansions into Equation (464 ) to obtain the projections of the singular electromagnetic field $F S = ∇ αAS − ∇ βAS αβ β α$ in the same tetrad $(eα,eα) 0 a$ that was employed in Section 5.2.3. This gives

F S(u, r,Ωa) ≡ F S (x )eα(x)eβ(x) a0 αβ a 0 -e e-( b ) 2- 1- b c 1- ( b b c) = r2Ωa − r aa − abΩ Ωa − 3e˙aa + 3 eRb0c0Ω Ω Ωa − 6e 5Ra0b0Ω + Rab0cΩ Ω 1 ( b c ) 1 b + --e 5R00 + RbcΩ Ω + R Ωa − --eRabΩ + 𝒪 (r), (469 ) S a S12 α β 6 F ab(u, r,Ω ) ≡ F αβ(x )ea(x)eb(x) e 1 c = --(aaΩb − Ωaab ) + -e(Ra0bc − Rb0ac + Ra0c0Ωb − ΩaRb0c0)Ω r 2 − 1e(Ra0 Ωb − ΩaRb0 ) + 𝒪 (r), (470 ) 2

in which all frame components are evaluated at the retarded point $x′$ . Comparison of these expressions with Equations (451

) and (452

) reveals that the retarded and singular fields share the same singularity structure.

The difference between the retarded field of Equations (451 , 452 ) and the singular field of Equations (469 , 470 ) defines the radiative field $F Rαβ(x)$ . Its tetrad components are

R 2- 1- tail F a0 = 3 e˙aa + 3eRa0 + Fa0 + 𝒪(r), (471 ) F R = F tail+ 𝒪 (r), (472 ) ab ab

and we see that $F Rαβ$ is a smooth tensor field on the world line. There is therefore no obstacle in evaluating the radiative field directly at $x = x ′$ , where the tetrad $(eα ,eα) 0 a$ becomes $(u α′,eα′) a$ . Reconstructing the field at $′ x$ from its frame components, we obtain

where the tail term can be copied from Equation (454

The tensors appearing in Equation (473

) all refer to the retarded point $′ x ≡ z(u)$ , which now stands for an arbitrary point on the world line $γ$ .

5.2.6 Equations of motion

The retarded field $Fαβ$ of a point electric charge is singular on the world line, and this behaviour makes it difficult to understand how the field is supposed to act on the particle and exert a force. The field’s singularity structure was analyzed in Sections 5.2.3 and 5.2.4, and in Section 5.2.5 it was shown to originate from the singular field $S Fαβ$ ; the radiative field $R S Fαβ = F αβ − Fαβ$ was then shown to be smooth on the world line.

To make sense of the retarded field’s action on the particle we follow the discussion of Section 5.1.6 and temporarily picture the electric charge as a spherical hollow shell; the shell’s radius is $s0$ in Fermi normal coordinates, and it is independent of the angles contained in the unit vector $ωa$ . The net force acting at proper time $τ$ on this shell is proportional to the average of $a F αβ(τ,s0,ω )$ over the shell’s surface. This was worked out at the end of Section 5.2.4, and ignoring terms that disappear in the limit $s0 → 0$ , we obtain

where

is formally a divergent quantity and

is the tail part of the force; all tensors in Equation (475

) are evaluated at an arbitrary point $z(τ)$ on the world line.

Substituting Equations (475 ) and (477 ) into Equation (439 ) gives rise to the equations of motion for the electric charge

with $m$ denoting the (also formally divergent) bare mass of the particle. We see that $m$ and $δm$ combine in Equation (478

) to form the particle’s observed mass $mobs$ , which is finite and gives a true measure of the particle’s inertia. All diverging quantities have thus disappeared into the procedure of mass renormalization.

Apart from the term proportional to $δm$ , the averaged force of Equation (475 ) has exactly the same form as the force that arises from the radiative field of Equation (473 ), which we express as

The force acting on the point particle can therefore be thought of as originating from the (smooth) radiative field, while the singular field simply contributes to the particle’s inertia. After mass renormalization, Equation (478

) is equivalent to the statement

where we have dropped the superfluous label “obs” on the particle’s observed mass.

For the final expression of the equations of motion we follow the discussion of Section 5.1.6 and allow an external force $μ fext$ to act on the particle, and we replace, on the right-hand side of the equations, the acceleration vector by $μ fext∕m$ . This produces

μ ( ν ) ∫ τ− m Du---= f μ + e2(δμ + u μuν) -2--Df-ext-+ 1R ν uλ + 2e2u ν ∇ [μG ν]′ (z(τ),z(τ′))uλ′ dτ′, dτ ext ν 3m dτ 3 λ − ∞ +λ (481 )

in which $m$ denotes the observed inertial mass of the electric charge and all tensors are evaluated at $z(τ)$ , the current position of the particle on the world line; the primed indices in the tail integral refer to the point $z(τ′)$ , which represents a prior position. We recall that the integration must be cut short at $′ − + τ = τ ≡ τ − 0$ to avoid the singular behaviour of the retarded Green’s function at coincidence; this procedure was justified at the beginning of Section 5.2.3. Equation (481

) was first derived (without the Ricci-tensor term) by Bryce S. DeWitt and Robert W. Brehme in 1960 [24

], and then corrected by J.M. Hobbs in 1968 [29 ]. An alternative derivation was produced by Theodore C. Quinn and Robert M. Wald in 1997 [49

]. In a subsequent publication [50

], Quinn and Wald proved that the total work done by the electromagnetic self-force matches the energy radiated away by the particle.