Motion of a point mass

5.3 Motion of a point mass

5.3.1 Dynamics of a point mass

In this section we consider the motion of a point particle of mass $m$ subjected to its own gravitational field. The particle moves on a world line $γ$ in a curved spacetime whose background metric $gαβ$ is assumed to be a vacuum solution to the Einstein field equations. We shall suppose that $m$ is small, so that the perturbation $hαβ$ created by the particle can also be considered to be small; it will obey a linear wave equation in the background spacetime. This linearization of the field equations will allow us to fit the problem of determining the motion of a point mass within the framework developed in Sections 5.1 and 5.2, and we shall obtain the equations of motion by following the same general line of reasoning. We shall find that $γ$ is not a geodesic of the background spacetime because $hαβ$ acts on the particle and induces an acceleration of order $m$ ; the motion is geodesic in the test-mass limit only.

Our discussion in this first section is largely formal: As in Sections 5.1.1 and 5.2.1 we insert the point particle in the background spacetime and ignore the fact that the field it produces is singular on the world line. To make sense of the formal equations of motion will be our goal in the following Sections 5.3.2, 5.3.3, 5.3.4, 5.3.5, 5.3.6, and 5.3.7. The problem of determining the motion of a small mass in a background spacetime will be reconsidered in Section 5.4 from a different and more satisfying premise: There the small body will be modeled as a black hole instead of as a point particle, and the singular behaviour of the perturbation will automatically be eliminated.

Let a point particle of mass $m$ move on a world line $γ$ in a curved spacetime with metric $gαβ$ . This is the total metric of the perturbed spacetime, and it depends on $m$ as well as all other relevant parameters. At a later stage of the discussion the total metric will be broken down into a “background” part $g αβ$ that is independent of $m$ , and a “perturbation” part $h αβ$ that is proportional to $m$ . The world line is described by relations $μ z (λ)$ in which $λ$ is an arbitrary parameter – this will later be identified with proper time $τ$ in the background spacetime. In this and the following sections we will use $sans-serif$ symbols to denote tensors that refer to the perturbed spacetime; tensors in the background spacetime will be denoted, as usual, by italic symbols.

The particle’s action functional is

where $˙zμ = dzμ∕d λ$ is tangent to the world line and the metric is evaluated at $z$ . We assume that the particle provides the only source of matter in the spacetime – an explanation will be provided at the end of this section – so that the Einstein field equations take the form of

where $Gαβ$ is the Einstein tensor constructed from $gαβ$ , and

is the particle’s stress-energy tensor, obtained by functional differentiation of $S particle$ with respect to $gαβ(x )$ ; the parallel propagators appear naturally by expressing $gμν$ as $α β g μg νgαβ$ .

On a formal level the metric $gαβ$ is obtained by solving the Einstein field equations, and the world line is determined by solving the equations of energy-momentum conservation, which follow from the field equations. From Equations (81 , 260 , 484 ) we obtain

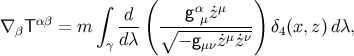
∫ ( α μ ) αβ -d- ∘---gμ-˙z----- ∇ βT = m γdλ − g μν ˙zμ˙zν δ4(x,z )dλ,

and additional manipulations reduce this to

∫ α ( μ ) ∇ Tαβ = m ∘---g-μ----- Dz˙-− k˙zμ δ (x,z)d λ, β γ − gμν ˙zμ˙zν d λ 4

where $μ Dz˙∕d λ$ is the covariant acceleration and $k$ is a scalar field on the world line. Energy-momentum conservation therefore produces the geodesic equation

and

measures the failure of $λ$ to be an affine parameter on the geodesic $γ$ .

At this stage we begin treating $m$ as a formal expansion parameter, and we write

with $gαβ$ denoting the $m → 0$ limit of the total metric $gαβ$ , and $h αβ = 𝒪 (m )$ the first-order correction. We shall refer to $gαβ$ as the “metric of the background spacetime” and to $hαβ$ as the “perturbation” produced by the particle. We similarly write

for the Einstein tensor, and

for the particle’s stress-energy tensor. The leading term $T αβ(x)$ describes the stress-energy tensor of a test particle of mass $m$ that moves on a world line $γ$ in a background spacetime with metric $gαβ$ . If we choose $λ$ to be proper time $τ$ as measured in this spacetime, then Equation (484

) implies

where $uμ(τ) = dzμ∕d τ$ is the particle’s four-velocity.

We have already stated that the particle is the only source of matter in the spacetime, and the metric $gαβ$ must therefore be a solution to the vacuum field equations: $αβ G [g] = 0$ . Equations (483 , 488 , (489 ) then imply $H αβ[g; h] = 8 πT αβ$ , in which both sides of the equation are of order $m$ . To simplify the expression of the first-order correction to the Einstein tensor we introduce the trace-reversed gravitational potentials

and we impose the Lorenz gauge condition

Here and below it is understood that indices are lowered and raised with the background metric and its inverse, respectively, and that covariant differentiation refers to a connection that is compatible with $gα β$ . We then have $αβ 1 αβ α β γδ H = − 2(□γ + 2Rγ δ γ )$ , and Equation (483

) reduces to

where $αβ □ = g ∇ α∇ β$ is the wave operator and $αβ T$ is defined by Equation (490

). We have here a linear wave equation for the potentials $γαβ$ , and this equation can be placed on an equal footing with Equation (385

) for the potential $Φ$ associated with a point scalar charge, and Equation (441

) for the vector potential $A α$ associated with a point electric charge.

The equations of motion for the point mass are obtained by substituting the expansion of Equation (487 ) into Equations (485 ) and (486 ). The perturbed connection is easily computed to be $Γ αβγ + 12(h αβ;γ + hαγ;β − hβγ;α)$ , and this leads to

μ μ Dz˙-= Du---+ 1-(h μ + h μ − h ;μ)u νuλ + 𝒪 (m2 ), d τ dτ 2 ν;λ λ;ν νλ

having once more selected proper time $τ$ (as measured in the background spacetime) as the parameter on the world line. On the other hand, Equation (486 ) gives

1 k = − --hνλ;ρuνu λuρ − hνλuνaλ + 𝒪 (m2 ), 2

where $λ λ a = Du ∕dτ$ is the particle’s acceleration vector. Since it is clear that the acceleration will be of order $m$ , the second term can be discarded and we obtain

μ Du--- = − 1-(hμ + hμ − h ;μ + uμh uρ) uνuλ + 𝒪 (m2 ). d τ 2 ν;λ λ;ν νλ νλ;ρ

Keeping the error term implicit, we shall express this in the equivalent form

which emphasizes the fact that the acceleration is orthogonal to the four-velocity.

It should be clear that Equation (494 ) is valid only in a formal sense, because the potentials obtained from Equations (493 ) diverge on the world line. The nonlinearity of the Einstein field equations makes this problem even worse here than for the scalar and electromagnetic cases, because the singular behaviour of the perturbation might render meaningless a formal expansion of $gαβ$ in powers of $m$ . Ignoring this issue for the time being (we shall return to it in Section 5.4), we will proceed as in Sections 5.1 and 5.2 and attempt, with a careful analysis of the field’s singularity structure, to make sense of these equations.

To conclude this section I should explain why it is desirable to restrict our discussion to spacetimes that contain no matter except for the point particle. Suppose, in contradiction with this assumption, that the background spacetime contains a distribution of matter around which the particle is moving. (The corresponding vacuum situation has the particle moving around a black hole. Notice that we are still assuming that the particle moves in a region of spacetime in which there is no matter; the issue is whether we can allow for a distribution of matter somewhere else.) Suppose also that the matter distribution is described by a collection of matter fields $Ψ$ . Then the field equations satisfied by the matter have the schematic form $E [Ψ;g ] = 0$ , and the metric is determined by the Einstein field equations $G[g] = 8πM [Ψ; g]$ , in which $M [Ψ; g]$ stands for the matter’s stress-energy tensor. We now insert the point particle in the spacetime, and recognize that this displaces the background solution $(Ψ,g)$ to a new solution ( $Ψ + δΨ, g + δg)$ . The perturbations are determined by the coupled set of equations $E [Ψ + δΨ; g + δg] = 0$ and $G [g + δg ] = 8πM [Ψ + δΨ; g + δg] + 8πT [g ]$ . After linearization these take the form of

E Ψ ⋅ δΨ + Eg ⋅ δg = 0, Gg ⋅ δg = 8π (M Ψ ⋅ δΨ + Mg ⋅ δg + T ),

where $EΨ$ , $Eg$ , $M Φ$ , and $Mg$ are suitable differential operators acting on the perturbations. This is a coupled set of partial differential equations for the perturbations $δΨ$ and $δg$ . These equations are linear, but they are much more difficult to deal with than the single equation for $δg$ that was obtained in the vacuum case. And although it is still possible to solve the coupled set of equations via a Green’s function technique, the degree of difficulty is such that we will not attempt this here. We shall, therefore, continue to restrict our attention to the case of a point particle moving in a vacuum (globally Ricci-flat) background spacetime.

5.3.2 Retarded potentials near the world line

The retarded solution to Equation (493 ) is $γ αβ(x) = 4∫ G αβ (x,x′)Tγ′δ′(x′)√−-g′d4x ′ + γ′δ′$ , where $αβ G + γ′δ′(x,x′)$ is the retarded Green’s function introduced in Section 4.5. After substitution of the stress-energy tensor of Equation (490 ) we obtain

in which $zμ(τ )$ gives the description of the world line $γ$ and $u μ = dzμ∕d τ$ . Because the retarded Green’s function is defined globally in the entire background spacetime, Equation (495

) describes the gravitational perturbation created by the particle at any point $x$ in that spacetime.

For a more concrete expression we must take $x$ to be in a neighbourhood of the world line. The following manipulations follow closely those performed in Section 5.1.2 for the case of a scalar charge, and in Section 5.2.2 for the case of an electric charge. Because these manipulations are by now familiar, it will be sufficient here to present only the main steps. There are two important simplifications that occur in the case of a massive particle. First, for the purposes of computing $αβ γ (x )$ to first order in $m$ , it is sufficient to take the world line to be a geodesic of the background spacetime: The deviations from geodesic motion that we are in the process of calculating are themselves of order $m$ and would affect $γαβ (x )$ at order $m2$ only. We shall therefore be allowed to set

in our computations. Second, because we take $g αβ$ to be a solution to the vacuum field equations, we are also allowed to set

in our computations.

With the understanding that $x$ is close to the world line (refer back to Figure 9 ), we substitute the Hadamard construction of Equation (352 ) into Equation (495 ) and integrate over the portion of $γ$ that is contained in $𝒩 (x)$ . The result is

in which primed indices refer to the retarded point $′ x ≡ z (u )$ associated with $x$ , $α′ r ≡ σ α′u$ is the retarded distance from $′ x$ to $x$ , and $τ<$ is the proper time at which $γ$ enters $𝒩 (x )$ from the past.

In the following Sections 5.3.3, 5.3.4, 5.3.5, 5.3.6, and 5.3.7, we shall refer to $γαβ(x )$ as the gravitational potentials at $x$ produced by a particle of mass $m$ moving on the world line $γ$ , and to $γαβ;γ(x)$ as the gravitational field at $x$ . To compute this is our next task.

5.3.3 Gravitational field in retarded coordinates

Keeping in mind that $x′$ and $x$ are related by $σ(x,x′) = 0$ , a straightforward computation reveals that the covariant derivatives of the gravitational potentials are given by

4m-- α′ β′ 4m-- α′ β′ 4m-- α′ β′ γ′ γαβ;γ(x) = − r2 U αβα′β′u u ∂γr + r U αβα′β′;γu u + r U αβα′β′;γ′u u u ∂γu α′ β′ tail + 4mV αβα′β′u u ∂γu + γαβγ(x), (499 )

where the “tail integral” is defined by

∫ u ∫ τ< γtαaβilγ(x) = 4m ∇ γV αβμν(x, z)uμuν dτ + 4m ∇ γG+ αβμν(x,z)uμuν dτ τ< −∞ ∫ u− = 4m ∇ γG+ αβμν(x, z)uμuν dτ. (500 ) −∞

The second form of the definition, in which the integration is cut short at $τ = u− ≡ u − 0+$ to avoid the singular behaviour of the retarded Green’s function at $σ = 0$ , is equivalent to the first form.

We wish to express $γαβ;γ(x)$ in the retarded coordinates of Section 3.3, as an expansion in powers of $r$ . For this purpose we decompose the field in the tetrad $(eα0,eαa)$ that is obtained by parallel transport of $(uα′,eα′) a$ on the null geodesic that links $x$ to $x′$ ; this construction is detailed in Section 3.3. Note that throughout this section we set $ωab = 0$ , where $ωab$ is the rotation tensor defined by Equation (138 ): The tetrad vectors $α′ ea$ are taken to be parallel transported on $γ$ . We recall from Equation (141 ) that the parallel propagator can be expressed as $′ ′ ′ gαα = uα e0α + eαa eaα$ . The expansion relies on Equation (166 ) for $∂γu$ and Equation (168 ) for $∂γr$ , both specialized to the case of geodesic motio, $aa = 0$ . We shall also need

which follows from Equation (358

which follow from Equations (359

) and (360

), respectively, as well as the relation $′ ′ ′ σα = − r(uα + Ωae αa )$ first encountered in Equation (144

). And finally, we shall need

which follows from Equation (362

Making these substitutions in Equation (484 ) and projecting against various members of the tetrad gives

γ (u,r,Ωa ) ≡ γ (x)eα(x)eβ(x )eγ(x ) = 2mR ΩaΩb + γtail + 𝒪 (r), (505 ) 000 αβ;γ 0 0 0 a0b0 000 γ0b0(u,r,Ωa ) ≡ γ αβ;γ(x)eα0(x)eβb(x )eγ0(x ) = − 4mRb0c0 Ωc + γt0abi0l+ 𝒪 (r), (506 ) a α β γ tail γab0(u,r,Ω ) ≡ γ αβ;γ(x)ea(x)eb(x )e0(x ) = 4mRa0b0 + γab0 + 𝒪 (r), (507 ) γ00c(u,r,Ωa ) ≡ γ αβ;γ(x)eα0(x)eβ0(x )eγc(x ) [( ) ] = − 4m 1-+ 1Ra0b0Ωa Ωb Ωc + 1Rc0b0Ωb − 1-Rca0bΩaΩb + γta00icl+ 𝒪 (r), (508 ) r2 3 6 6 γ (u,r,Ωa ) ≡ γ (x)eα(x)eβ(x )eγ(x ) 0bc αβ;γ( 0 b cd d ) tail = 2m Rb0c0 + Rb0cdΩ + Rb0d0Ω Ωc + γ 0bc + 𝒪 (r), (509 ) γ (u,r,Ωa ) ≡ γ (x)eα(x)eβ(x )eγ(x ) = − 4mR Ω + γtail+ 𝒪 (r), (510 ) abc αβ;γ a b c a0b0 c abc

where, for example, $′ ′ ′ ′ Ra0b0(u) ≡ R α′γ′β′δ′eαa u γeβb uδ$ are frame components of the Riemann tensor evaluated at $x′ ≡ z(u)$ . We have also introduced the frame components of the tail part of the gravitational field, which are obtained from Equation (500

) evaluated at $x ′$ instead of $x$ ; for example, $tail α′ β′ γ′ tail ′ γ000 = u u u γα′β′γ′(x )$ . We may note here that while $γ00c$ is the only component of the gravitational field that diverges when $r → 0$ , the other components are nevertheless singular because of their dependence on the unit vector $Ωa$ ; the only exception is $γab0$ , which is smooth.

5.3.4 Gravitational field in Fermi normal coordinates

The translation of the results contained in Equations (505 , 506 , 507 , 508 , 509 , 510 ) into the Fermi normal coordinates of Section 3.2 proceeds as in Sections 5.1.4 and 5.2.4, but is simplified by the fact that here the world line can be taken to be a geodesic. We may thus set $a = ˙a = ˙a = 0 a 0 a$ in Equations (224 ) and (225 ) that relate the tetrad $α α (¯e0,¯ea )$ to $α α (e0,ea)$ , as well as in Equations (221 , 222 , 223 ) that relate the Fermi normal coordinates $a (t,s,ω )$ to the retarded coordinates. We recall that the Fermi normal coordinates refer to a point $¯x ≡ z(t)$ on the world line that is linked to $x$ by a spacelike geodesic that intersects $γ$ orthogonally.

The translated results are

¯γ (t,s,ωa) ≡ γ (x)¯eα(x)¯eβ(x)¯eγ(x ) = γ¯tail+ 𝒪 (s), (511 ) 000 αβ;γ 0 0 0 000 ¯γ0b0(t,s,ωa) ≡ γ αβ;γ(x)¯eα0(x)¯eβb(x)¯eγ0(x ) = − 4mRb0c0 ωc + ¯γt0abil0 + 𝒪(s), (512 ) a α β γ tail ¯γab0(t,s,ω ) ≡ γ αβ;γ(x)¯ea(x)¯eb(x)¯e0(x ) = 4mRa0b0 + ¯γab0 + 𝒪 (s ), (513 ) ¯γ00c(t,s,ωa) ≡ γ αβ;γ(x)¯eα0(x)¯eβ0(x)¯eγc(x ) [( ) ] = − 4m 1-− 1Ra0b0ωa ωb ωc + 1-Rc0b0ωb + ¯γta0i0cl+ 𝒪 (s), (514 ) s2 6 3 ¯γ (t,s,ωa) ≡ γ (x)¯eα(x)¯eβ(x)¯eγ(x ) = 2m (R + R ωd ) + ¯γtail+ 𝒪 (s), (515 ) 0bc αβ;γ 0 b c b0c0 b0cd 0bc ¯γabc(t,s,ωa) ≡ γ αβ;γ(x)¯eαa(x)¯eβb(x)¯eγc(x ) = − 4mRa0b0 ωc + ¯γtaabilc + 𝒪 (s), (516 )

where all frame components are now evaluated at $¯x$ instead of $′ x$ .

It is then a simple matter to average these results over a two-surface of constant $t$ and $s$ . Using the area element of Equation (404 ) and definitions analogous to those of Equation (405 ), we obtain

tail ⟨¯γ000⟩ = ¯γ 000 + 𝒪 (s), (517 ) ⟨¯γ0b0⟩ = ¯γta0bi0l+ 𝒪 (s), (518 ) tail ⟨¯γab0⟩ = 4mRa0b0 + ¯γab0 + 𝒪 (s), (519 ) ⟨¯γ00c⟩ = ¯γta00icl+ 𝒪 (s), (520 ) tail ⟨¯γ0bc⟩ = 2mRb0c0 + ¯γ0bc + 𝒪(s), (521 ) ⟨¯γabc⟩ = ¯γtaabicl+ 𝒪 (s). (522 )

The averaged gravitational field is smooth in the limit $s → 0$ , in which the tetrad $α α (¯e0,¯ea)$ coincides with $α¯ ¯α (u ,ea)$ . Reconstructing the field at $¯x$ from its frame components gives

where the tail term can be copied from Equation (500

The tensors that appear in Equation (523

) all refer to the simultaneous point $¯x ≡ z(t)$ , which can now be treated as an arbitrary point on the world line $γ$ .

5.3.5 Singular and radiative fields

The singular gravitational potentials

are solutions to the wave equation of Equation (493

); the singular Green’s function was introduced in Section 4.5.4. We will see that the singular field $S γαβ;γ$ reproduces the singular behaviour of the retarded solution near the world line, and that the difference, $γR = γαβ;γ − γS αβ;γ α β;γ$ , is smooth on the world line.

To evaluate the integral of Equation (525 ) we take $x$ to be close to the world line (see Figure 9 ), and we invoke Equation (373 ) as well as the Hadamard construction of Equation (379 ). This gives

where primed indices refer to the retarded point $′ x ≡ z(u)$ , double-primed indices refer to the advanced point $′′ x ≡ z (v )$ , and where $α′′ radv ≡ − σ α′′u$ is the advanced distance between $x$ and the world line.

Differentiation of Equation (526 ) yields

γS (x) = − 2m--U ′ ′uα ′uβ′∂ r − -2m--U ′′ ′′uα′′uβ′′∂ r + 2m-U ′ ′ uα′u β′ αβ;γ r2 αβα β γ radv2 αβα β γ adv r αβα β;γ 2m ′ ′ ′ 2m ′′ ′′ 2m ′′ ′′ ′′ + ---U αβα′β′;γ′u αuβu γ∂γu + ----Uαβα′′β′′;γuα uβ + ----Uαβα′′β′′;γ′′u αu βuγ ∂ γv r radv ra∫dvv ′ ′α′ β′ ′′ ′′ α′′ β′′ μ ν + 2mV αβα βu u ∂γu − 2mV αβα β u u ∂γv − 2m u∇ γV αβμν(x, z)u u dτ, (527 )

and we would like to express this as an expansion in powers of $r$ . For this we will rely on results already established in Section 5.3.3, as well as additional expansions that will involve the advanced point $x′′$ . We recall that a relation between retarded and advanced times was worked out in Equation (229

), that an expression for the advanced distance was displayed in Equation (230

), and that Equations (231

) and (232

) give expansions for $∂γv$ and $∂γradv$ , respectively; these results can be simplified by setting $aa = ˙a0 = ˙aa = 0$ , which is appropriate in this computation.

To derive an expansion for $α′′ β′′ U αβα′′β′′u u$ we follow the general method of Section 3.4.4 and introduce the functions $Uαβ(τ) ≡ U αβμν(x,z)uμu ν$ . We have that

′′ ′′ 1 ( ) Uαβα′′β′′u α uβ ≡ Uαβ (v ) = U αβ(u) + U˙αβ (u )Δ′ +-¨U αβ(u)Δ′2 + O Δ′3 , 2

where overdots indicate differentiation with respect to $τ$ and $Δ′ ≡ v − u$ . The leading term $′ ′ U αβ(u) ≡ Uα βα′β′uα uβ$ was worked out in Equation (501 ), and the derivatives of $U αβ(τ)$ are given by

˙Uαβ(u) = U αβα′β′;γ′uα′uβ′uγ′ = gα′gβ′ [rR α′0d0Ωdu β′ + 𝒪 (r2)] (α β)

and

α′ β′ γ′δ′ ¨U αβ(u) = Uαβα′β′;γ′δ′u u u u = 𝒪 (r),

according to Equations (503 ) and (360 ). Combining these results together with Equation (229 ) for $Δ ′$ gives

which should be compared with Equation (501

). It should be emphasized that in Equation (528

) and all equations below, all frame components are evaluated at the retarded point $′ x$ , and not at the advanced point. The preceding computation gives us also an expansion for

α′β′′ γ′′ ′ ′2 U αβα′′β′′;γ′′u u u = ˙Uαβ(u ) + U¨αβ(u)Δ + 𝒪 (Δ ),

which becomes

and which is identical to Equation (503

We proceed similarly to obtain an expansion for $′′ ′′ α′′ β′′ U αβα β ;γu u$ . Here we introduce the functions $μ ν U αβγ(τ) ≡ Uαβμν;γu u$ and express $α′′ β′′ U αβα′′β′′;γu u$ as $˙ ′ ′2 Uαβγ(v) = U αβγ(u ) + U αβγ(u)Δ + 𝒪 (Δ )$ . The leading term $′ ′ U αβγ(u) ≡ Uαβα ′β′;γuα uβ$ was computed in Equation (502 ), and

′ ′ ′ ′ ′ ′ ˙Uαβγ(u) = U αβα′β′;γγ′uα uβ uγ = g α(αgββ)g γγ [R α′0γ′0uβ′ + 𝒪 (r)]

follows from Equation (359 ). Combining these results together with Equation (229 ) for $′ Δ$ gives

and this should be compared with Equation (502

). The last expansion we shall need is

which is identical to Equation (504

We obtain the frame components of the singular gravitational field by substituting these expansions into Equation (527 ) and projecting against the tetrad $α α (e0,ea)$ . After some algebra we arrive at

γS000(u,r,Ωa ) ≡ γSαβ;γ(x )eα0(x)eβ0(x)eγ0(x) = 2mRa0b0 Ωa Ωb + 𝒪 (r), (532 ) S a S α β γ c γ0b0(u,r,Ω ) ≡ γαβ;γ(x )e0(x)eb(x)e0(x) = − 4mRb0c0 Ω + 𝒪 (r), (533 ) γS (u,r,Ωa ) ≡ γS (x )eα(x)eβ(x)eγ(x) = 𝒪 (r), (534 ) ab0 αβ;γ a b 0 γS00c(u,r,Ωa ) ≡ γSαβ;γ(x )eα0(x)eβ0(x)eγc(x) [( ) ] = − 4m -1 + 1-Ra0b0ΩaΩb Ωc + 1-Rc0b0Ωb − 1Rca0bΩa Ωb + 𝒪 (r), (535 ) r2 3 6 6 γS (u,r,Ωa ) ≡ γS (x )eα(x)eβ(x)eγ(x) = 2m (R Ωd + R ΩdΩ ) + 𝒪 (r), (536 ) 0bc αβ;γ 0 b c b0cd b0d0 c γSabc(u,r,Ωa ) ≡ γSαβ;γ(x )eαa(x)eβb(x)eγc(x) = − 4mRa0b0 Ωc + 𝒪 (r), (537 )

in which all frame components are evaluated at the retarded point $x′$ . Comparison of these expressions with Equations (505

, 506

, 507

, 508

, 509

, 510

) reveals identical singularity structures for the retarded and singular gravitational fields.

The difference between the retarded field of Equations (505 , 506 , 507 , 508 , 509 , 510 ) and the singular field of Equations (532 , 533 , 534 , 535 , 536 , 537 ) defines the radiative gravitational field $γRαβ;γ$ . Its tetrad components are

γR = γtail+ 𝒪 (r), (538 ) 0R00 00ta0il γ0b0 = γ 0b0 + 𝒪 (r), (539 ) γR = 4mR + γtail + 𝒪 (r), (540 ) aRb0 taila0b0 ab0 γ00c = γ 00c + 𝒪 (r), (541 ) γR = 2mRb0c0 + γtail+ 𝒪 (r), (542 ) 0Rbc tail 0bc γabc = γ abc + 𝒪 (r), (543 )

and we see that $γR α β;γ$ is smooth in the limit $r → 0$ . We may therefore evaluate the radiative field directly at $′ x = x$ , where the tetrad $α α (e0,ea)$ coincides with $α′ α′ (u ,ea )$ . After reconstructing the field at $′ x$ from its frame components, we obtain

where the tail term can be copied from Equation (500

The tensors that appear in Equation (545

) all refer to the retarded point $x′ ≡ z (u )$ , which can now be treated as an arbitrary point on the world line $γ$ .

5.3.6 Equations of motion

The retarded gravitational field $γαβ;γ$ of a point particle is singular on the world line, and this behaviour makes it difficult to understand how the field is supposed to act on the particle and influence its motion. The field’s singularity structure was analyzed in Sections 5.3.3 and 5.3.4, and in Section 5.3.5 it was shown to originate from the singular field $S γαβ;γ$ ; the radiative field $R γαβ;γ$ was then shown to be smooth on the world line.

To make sense of the retarded field’s action on the particle we can follow the discussions of Section 5.1.6 and 5.2.6 and postulate that the self gravitational field of the point particle is either $⟨γ ⟩ μν;λ$ , as worked out in Equation (523 ), or $R γμν;λ$ , as worked out in Equation (544 ). These regularized fields are both given by

and

in which all tensors are now evaluated at an arbitrary point $z(τ)$ on the world line $γ$ .

The actual gravitational perturbation $hαβ$ is obtained by inverting Equation (491 ), which leads to $h = γ − 1g γρ μν;λ μν;γ 2 μν ρ;λ$ . Substituting Equation (546 ) yields

where the tail term is given by the trace-reversed counterpart to Equation (547

When this regularized field is substituted into Equation (494

), we find that the terms that depend on the Riemann tensor cancel out, and we are left with

We see that only the tail term is involved in the final form of the equations of motion. The tail integral of Equation (549

) involves the current position $z(τ)$ of the particle, at which all tensors with unprimed indices are evaluated, as well as all prior positions $′ z(τ )$ , at which all tensors with primed indices are evaluated. The tail integral is cut short at $τ′ = τ− ≡ τ − 0+$ to avoid the singular behaviour of the retarded Green’s function at coincidence; this limiting procedure was justified at the beginning of Section 5.3.3.

Equation (550 ) was first derived by Yasushi Mino, Misao Sasaki, and Takahiro Tanaka in 1997 [39 ]. (An incomplete treatment had been given previously by Morette-DeWitt and Ging [42 ].) An alternative derivation was then produced, also in 1997, by Theodore C. Quinn and Robert M. Wald [49 ]. These equations are now known as the MiSaTaQuWa equations of motion. It should be noted that Equation (550 ) is formally equivalent to the statement that the point particle moves on a geodesic in a spacetime with metric $R gαβ + hαβ$ , where $R hα β$ is the radiative metric perturbation obtained by trace-reversal of the potentials $γRαβ ≡ γαβ − γSαβ$ ; this perturbed metric is smooth on the world line, and it is a solution to the vacuum field equations. This elegant interpretation of the MiSaTaQuWa equations was proposed in 2002 by Steven Detweiler and Bernard F. Whiting [23 ]. Quinn and Wald [50 ] have shown that under some conditions, the total work done by the gravitational self-force is equal to the energy radiated (in gravitational waves) by the particle.

5.3.7 Gauge dependence of the equations of motion

The equations of motion derived in the preceding Section 5.3.6 refer to a specific choice of gauge for the metric perturbation $h αβ$ produced by a point particle of mass $m$ . We indeed recall that back at Equation (492 ) we imposed the Lorenz gauge condition $γαβ = 0 ;β$ on the gravitational potentials $1 γδ γαβ ≡ hαβ − 2(g h γδ)gαβ$ . By virtue of this condition we found that the potentials satisfy the wave equation of Equation (493 ) in a background spacetime with metric $g αβ$ . The hyperbolic nature of this equation allowed us to identify the retarded solution as the physically relevant solution, and the equations of motion were obtained by removing the singular part of the retarded field. It seems clear that the Lorenz condition is a most appropriate choice of gauge.

Once the equations of motion have been formulated, however, the freedom of performing a gauge transformation (either away from the Lorenz gauge, or within the class of Lorenz gauges) should be explored. A gauge transformation will affect the form of the equations of motion: These must depend on the choice of coordinates, and there is no reason to expect Equation (550 ) to be invariant under a gauge transformation. Our purpose in this section is to work out how the equations of motion change under such a transformation. This issue was first examined by Barack and Ori [8 ].

We introduce a coordinate transformation of the form

where $α x$ are the coordinates of the background spacetime, and $α ξ$ is a vector field that we take to be of order $m$ . We assume that $ξα$ is smooth in a neighbourhood of the world line $γ$ . The coordinate transformation changes the background metric according to

gα β → gαβ − ξα;β − ξβ;α + 𝒪 (m2),

and this change can be interpreted as a gauge transformation of the metric perturbation created by the moving particle:

This, in turn, produces a change in the particle’s acceleration,

where $aμ$ is the acceleration of Equation (550

) and $a[ξ]μ$ is the “gauge acceleration” generated by the vector field $ξα$ .

To compute the gauge acceleration we substitute Equation (552 ) into Equation (494 ), and we simplify the result by invoking Ricci’s identity, $ω ξλ;νρ − ξλ;ρν = R νρωλξ$ , and the fact that $μ a = 𝒪 (m )$ . The final expression is

where $2 ν 2 ν μ ρ D ξ ∕dτ = (ξ ;μu );ρu$ is the second covariant derivative of $ν ξ$ in the direction of the world line. The expression within the large brackets is familiar from the equation of geodesic deviation, which states that this quantity vanishes if $ξμ$ is a deviation vector between two neighbouring geodesics. Equation (553

), with $a[ξ]μ$ given by Equation (554

), is therefore a generalized version of this statement.