For a congruence of observers (or particles or photons) with four velocity 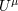 , the kinematic invariants fully describe
their relative motion. Consider those that, in a particular moment
, the kinematic invariants fully describe
their relative motion. Consider those that, in a particular moment 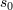 , occupy the surface of an infinitesimally small sphere.
Now, consider the deformation of that surface at a later moment
, occupy the surface of an infinitesimally small sphere.
Now, consider the deformation of that surface at a later moment 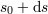 . The volume change
. The volume change 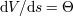 is called
expansion. The shear tensor
is called
expansion. The shear tensor 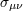 measures the ellipsoidal distortion of this sphere, and the vorticity tensor
measures the ellipsoidal distortion of this sphere, and the vorticity tensor 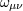 describes
its rotation (i.e., three independent rotations around three perpendicular axes). Expansion, shear, and vorticity are determined
by the tensor
describes
its rotation (i.e., three independent rotations around three perpendicular axes). Expansion, shear, and vorticity are determined
by the tensor 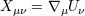 in the following way:
in the following way: 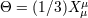 ,
, 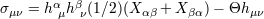 , and
, and
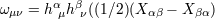 . Here
. Here 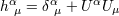 is the projection tensor. The acceleration
is the projection tensor. The acceleration 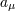 is also considered
a kinematic invariant.
is also considered
a kinematic invariant.
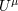 , the kinematic invariants fully describe
their relative motion. Consider those that, in a particular moment
, the kinematic invariants fully describe
their relative motion. Consider those that, in a particular moment 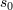 , occupy the surface of an infinitesimally small sphere.
Now, consider the deformation of that surface at a later moment
, occupy the surface of an infinitesimally small sphere.
Now, consider the deformation of that surface at a later moment 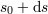 . The volume change
. The volume change 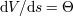 is called
expansion. The shear tensor
is called
expansion. The shear tensor 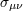 measures the ellipsoidal distortion of this sphere, and the vorticity tensor
measures the ellipsoidal distortion of this sphere, and the vorticity tensor 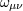 describes
its rotation (i.e., three independent rotations around three perpendicular axes). Expansion, shear, and vorticity are determined
by the tensor
describes
its rotation (i.e., three independent rotations around three perpendicular axes). Expansion, shear, and vorticity are determined
by the tensor 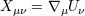 in the following way:
in the following way: 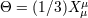 ,
, 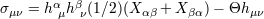 , and
, and
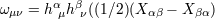 . Here
. Here 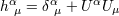 is the projection tensor. The acceleration
is the projection tensor. The acceleration 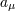 is also considered
a kinematic invariant.
is also considered
a kinematic invariant.