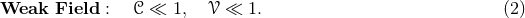1 Introduction
1.1 The importance of testing
The era of precision gravitational-wave astrophysics is at our doorstep. With it, a plethora of previously unavailable information will flood in, allowing for unprecedented astrophysical measurements and tests of fundamental theories. Nobody would question the importance of more precise astrophysical measurements, but one may wonder whether fundamental tests are truly necessary, considering the many successes of Einstein’s theory of general relativity (GR). Indeed, GR has passed many tests, including solar system ones, binary pulsar ones and cosmological ones (for a recent review, see [438*, 359*]).
What all of these tests have in common is that they sample the quasi-stationary, quasi-linear weak field regime of GR. That is, they sample the regime of spacetime where the gravitational field is weak relative to the mass-energy of the system, the characteristic velocities of gravitating bodies are small relative to the speed of light, and the gravitational field is stationary or quasi-stationary relative to the characteristic size of the system. A direct consequence of this is that gravitational waves emitted by weakly-gravitating, quasi-stationary sources are necessarily extremely weak. To make this more concrete, let us define the gravitational compactness as a measure of the strength of the gravitational field:
where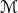 is the characteristic mass of the system,
is the characteristic mass of the system, 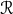 is the characteristic length scale associated with
gravitational radiation, and henceforth we set
is the characteristic length scale associated with
gravitational radiation, and henceforth we set 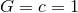 . For binary systems, the orbital separation serves
as this characteristic length scale. The strength of gravitational waves and the mutual gravitational
interaction between bodies scale linearly with this compactness measure. Let us also define the
characteristic velocities of such a system
. For binary systems, the orbital separation serves
as this characteristic length scale. The strength of gravitational waves and the mutual gravitational
interaction between bodies scale linearly with this compactness measure. Let us also define the
characteristic velocities of such a system 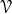 as a quantity related to the rate of change of the
gravitational field in the center of mass frame. We can then more formally define the weak
field as the region of spacetime where the following two conditions are simultaneously satisfied:
By similarity, the strong field is defined as the region of spacetime where both conditions in Eq. (2*) are not valid
simultaneously1.
as a quantity related to the rate of change of the
gravitational field in the center of mass frame. We can then more formally define the weak
field as the region of spacetime where the following two conditions are simultaneously satisfied:
By similarity, the strong field is defined as the region of spacetime where both conditions in Eq. (2*) are not valid
simultaneously1.
Let us provide some examples. For the Earth-Sun system, 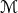 is essentially the mass of the sun, while
is essentially the mass of the sun, while
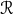 is the orbital separation, which leads to
is the orbital separation, which leads to 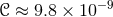 and
and 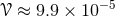 . Even if an object were
in a circular orbit at the surface of the sun, its gravitational compactness would be
. Even if an object were
in a circular orbit at the surface of the sun, its gravitational compactness would be 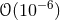 and its
characteristic velocity
and its
characteristic velocity 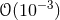 . Thus, we conclude that all solar-system experiments are necessarily
sampling the weak field regime of gravity. Similarly, for the binary pulsar J0737–3039 [298, 274*],
. Thus, we conclude that all solar-system experiments are necessarily
sampling the weak field regime of gravity. Similarly, for the binary pulsar J0737–3039 [298, 274*],
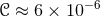 and
and 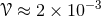 , where we have set the characteristic length
, where we have set the characteristic length 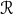 to the orbital
separation via
to the orbital
separation via ![ℛ ≈ [M P2∕(4π2 )]1∕3 ≈ 106 km](article15x.gif) , where
, where 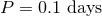 is the orbital period and
is the orbital period and
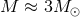 is the total mass. Although neutron stars are sources of strong gravity (the ratio of their mass
to their radius is of order one tenth), binary pulsars are most sensitive to the quasi-static part of the
post-Newtonian effective potential or to the leading-order (Newtonian piece) of the radiation-reaction
force. On the other hand, in compact binary coalescence the gravitational compactness and the
characteristic speed can reach values much closer to unity. Therefore, although in much of the
pulsar-timing literature binary pulsar timing is said to allow for strong-field tests of gravity,
gravitational information during compact binary coalescence would be a much-stronger–field
test.
is the total mass. Although neutron stars are sources of strong gravity (the ratio of their mass
to their radius is of order one tenth), binary pulsars are most sensitive to the quasi-static part of the
post-Newtonian effective potential or to the leading-order (Newtonian piece) of the radiation-reaction
force. On the other hand, in compact binary coalescence the gravitational compactness and the
characteristic speed can reach values much closer to unity. Therefore, although in much of the
pulsar-timing literature binary pulsar timing is said to allow for strong-field tests of gravity,
gravitational information during compact binary coalescence would be a much-stronger–field
test.
Even though current data does not give us access to the full non-linear and dynamical regime of GR, solar-system tests and binary-pulsar observations have served (and will continue to serve) an invaluable role in testing Einstein’s theory. Solar-system tests effectively cured an outbreak of modified gravity theories in the 1970s and 1980s, as summarized for example in [438*]. Binary pulsars were crucial as the first indirect detectors of gravitational waves, and later to kill certain theories, like Rosen’s bimetric gravity [365*], and heavily constrain others that predict dipolar energy loss, as we see in Sections 2 and 5. Binary pulsars are probes of GR in a certain sector of the strong field: in the dynamical but quasi-linear sector, verifying that compact objects move as described by a perturbative, post-Newtonian analysis to leading order. Binary pulsars can be used to test GR in the “strong field” only in the sense that they probe non-linear stellar-structure effects, but they say very little to nothing about non-linear radiative effects. Similarly, future electromagnetic observations of black-hole–accretion disks may probe GR in another strong-field sector: the non-linear but fully stationary regime, verifying that black holes are described by the Kerr metric. As of this writing, only gravitational waves will allow for tests of GR in the full strong-field regime, where gravity is both heavily non-linear and inherently dynamical.
No experiments exist to date that validate Einstein’s theory of GR in the highly-dynamical, strong-field region. Due to previous successes of GR, one might consider such validation unnecessary. However, as most scientists would agree, the role of science is to predict and verify and not to assume without proof. Moreover, the incompleteness of GR in the quantum regime, together with the somewhat unsatisfactory requirement of the dark sector of cosmology (including dark energy and dark matter), have prompted more than one physicist to consider deviations from GR more seriously. Gravitational waves will soon allow us to verify Einstein’s theory in a regime previously inaccessible to us, and as such, these tests are invaluable.
However, in many areas of physics GR is so ingrained that questioning its validity (even in a regime where Einstein’s theory has not yet been validated) is synonymous with heresy. Dimensional arguments are usually employed to argue that any quantum gravitational correction will necessarily and unavoidably be unobservable with gravitational waves, as the former are expected at a (Planck) scale that is inaccessible to gravitational-wave detectors. This rationalization is dangerous, as it introduces a theoretical bias in the analysis of new observations of the universe, thus reducing the potential for new discoveries. For example, if astrophysicists had followed such a rationalization when studying supernova data, they would not have discovered that the universe is expanding. Dimensional arguments suggest that the cosmological constant is over 100 orders of magnitude larger than the value required to agree with observations. When observing the universe for the first time in a completely new way, it seems more conservative to remain agnostic about what is expected and what is not, thus allowing the data itself to guide our efforts toward theoretically understanding the gravitational interaction.
1.2 Testing general relativity versus testing alternative theories
When testing GR, one considers Einstein’s theory as a null hypothesis and searches for generic deviations. On the other hand, when testing alternative theories one starts from a particular modified gravity model, develops its equations and solutions and then predicts certain observables that then might or might not agree with experiment. Similarly, one may define a bottom-up approach versus a top-down approach. In the former, one starts from some observables in an attempt to discover fundamental symmetries that may lead to a more complete theory, as was done when constructing the standard model of elementary particles. On the other hand, a top-down approach starts from some fundamental theory and then derives its consequence.
Both approaches possess strengths and weaknesses. In the top-down approach one has complete control over the theory under study, being able to write down the full equations of motion, answer questions about well-posedness and stability of solutions, and predict observables. But, as we see in Section 2, carrying out such an approach can be quixotic within any one model. What is worse, the lack of a complete and compelling alternative to GR makes choosing a particular modified theory difficult.
Given this, one might wish to attempt a bottom-up approach, where one considers a set of principles one wishes to test without explicit mention of any particular theory. One usually starts by assuming GR as a null-hypothesis and then considers deformations away from GR. The hope is that experiments will be sensitive to such deformations, thus either constraining the size of the deformations or pointing toward a possible inconsistency. But if experiments do confirm a GR deviation, a bottom-up approach fails at providing a given particular action from which to derive such a deformation. In fact, there can be several actions that lead to similar deformations, all of which can be consistent with the data within its experimental uncertainties.
Nonetheless, both approaches are complementary. The bottom-up approach draws inspiration from particular examples carried out in the top-down approach. Given a plausible measured deviation from GR within a bottom-up approach, one will still need to understand what plausible top-down theories can lead to such deviations. From this standpoint, then, both approaches are intrinsically intertwined and worth pursuing.
1.3 Gravitational-wave tests versus other tests of general relativity
Gravitational-wave tests differ from other tests of GR in many ways. Perhaps one of the most important differences is the spacetime regime gravitational waves sample. Indeed, as already mentioned, gravitational waves have access to the most extreme gravitational environments in nature. Moreover, gravitational waves travel essentially unimpeded from their source to Earth, and thus, they do not suffer from issues associated with obscuration. Gravitational waves also exist in the absence of luminous matter, thus allowing us to observe electromagnetically dark objects, such as black-hole inspirals.
This last point is particularly important as gravitational waves from inspiral–black-hole binaries are one of the cleanest astrophysical systems in nature. In the last stages of inspiral, when such gravitational waves would be detectable by ground-based interferometers, the evolution of a black-hole binary is essentially unaffected by any other matter or electromagnetic fields present in the system. As such, one does not need to deal with uncertainties associated with astrophysical matter. Unlike other tests of GR, such as those attempted with accretion-disk observations, black-hole–binary gravitational-wave tests may well be the cleanest probes of Einstein’s theory.
Of course, what is an advantage here, can also be a huge disadvantage in another context. Gravitational waves from compact binaries are intrinsically transient (they turn on for a certain amount of time and then shut off). This is unlike binary pulsar systems, for which astrophysicists have already collected tens of years of data. Moreover, gravitational wave tests rely on specific detections that cannot be anticipated beforehand. This is in contrast to Earth-based laboratory experiments, where one has complete control over the experimental setup. Finally, the intrinsic weakness of gravitational waves makes detection a very difficult task that requires complex data-analysis algorithms to extract signals from the noise. As such, gravitational-wave tests are limited by the signal-to-noise ratio and affected by systematics associated with the modeling of the waves, issues that are not as important in other loud astrophysical systems.
1.4 Ground-based vs space-based detectors and interferometers vs pulsar timing
This review article focuses only on ground-based detectors, by which we mean both gravitational-wave interferometers, such as the Laser Interferometer Gravitational Observatory (LIGO) [3, 2*, 217], Virgo [5, 6*] and the Einstein Telescope (ET) [361*, 377], as well as pulsar-timing arrays (for a recent review of gravitational-wave tests of GR with space-based detectors, see [183*, 446]). Ground-based detectors have the limitation of being contaminated by man-made and nature-made noise, such as ground and air traffic, logging, earthquakes, ocean tides and waves, which are clearly absent in space-based detectors. Ground-based detectors, however, have the clear benefit that they can be continuously upgraded and repaired in case of malfunction, which is obviously not possible with space-based detectors.
As far as tests of GR are concerned, there is a drastic difference in space-based and ground-based
detectors: the gravitational-wave frequencies these detectors are sensitive to. For various reasons that we
will not go into, space-based interferometers are likely to have million kilometer long arms, and thus, be
sensitive in the milli-Hz band. On the other hand, ground-based interferometers are bound to the surface
and curvature of the Earth, and thus, they have kilometer-long arms and are sensitive in the deca-
and hecta-Hz band. Different types of interferometers are then sensitive to different types of
gravitational-wave sources. For example, when considering binary coalescences, ground-based
interferometers are sensitive to late inspirals and mergers of neutron stars and stellar-mass black holes,
while space-based detectors will be sensitive to supermassive–black-hole binaries with masses around
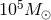 .
.
The impact of a different population of sources in tests of GR depends on the particular modified gravity theory considered. When studying quadratic gravity theories, as we see in Section 2, the Einstein–Hilbert action is modified by introducing higher-order curvature operators, which are naturally suppressed by powers of the inverse of the radius of curvature. Thus, space-based detectors will not be ideal at constraining these theories, as the radius of curvature of supermassive black holes is much larger than that of stellar-mass black holes at merger. Moreover, space-based detectors will not be sensitive to neutron-star–binary coalescences; they are sensitive to supermassive black-hole/neutron-star coalescences, where the radius of curvature of the system is controlled by the supermassive black hole.
On the other hand, space-based detectors are unique in their potential to probe the spacetime geometry of supermassive black holes through gravitational waves emitted during extreme–mass-ratio inspirals. These inspirals consist of a stellar-mass compact object in a generic decaying orbit around a supermassive black hole. Such inspirals produce millions of cycles of gravitational waves in the sensitivity band of space-based detectors (in fact, they can easily out-live the observation time!). Therefore, even small changes to the radiation-reaction force, or to the background geometry, can lead to noticeable effects in the waveform observable and thus strong tests of GR, albeit constrained to the radius of curvature of the supermassive black hole. For recent work on such systems and tests, see [23*, 370*, 371*, 263*, 196*, 50*, 289*, 182*, 390*, 471*, 31*, 297*, 184*, 116*, 93*, 183].
Space-based detectors also have the advantage of range, which is particularly important when considering theories where gravitons do not travel at light speed [316*]. Space-based detectors have a horizon distance much larger than ground-based detectors; the former can see black-hole mergers to redshifts of order 10 if there are any at such early times in the universe, while the latter are confined to events within redshift 1. Gravitational waves emitted from distant regions in spacetime need a longer time to propagate from the source to the detectors. Thus, theories that modify the propagation of gravitational waves will be best constrained by space-based type systems. Of course, such theories are also likely to modify the generation of gravitational waves, which ground-based detectors should also be sensitive to.
Another important difference between detectors is in their response to an impinging gravitational wave. Ground-based detectors, as we see in Section 3, cannot separate between the two possible scalar modes (the longitudinal and the breathing modes) of metric theories of gravity, due to an intrinsic degeneracy in the response functions. Space-based detectors in principle also possess this degeneracy, but they may be able to break it through Doppler modulation if the interferometer orbits the Sun. Pulsar-timing arrays, on the other hand, lack this degeneracy altogether, and thus, they can in principle constrain the existence of both modes independently.
Pulsar-timing arrays differ from interferometers in their potential to test GR mostly by the frequency space they are most sensitive to. The latter can observe the late inspiral and merger of compact binaries, while the former is restricted to the very early inspiral. This is why pulsar timing arrays do not need very accurate waveform templates that account for the highly-dynamical and non-linear nature of gravity to detect gravitational waves; leading-order quadrupole waveforms are sufficient [120]. In turn, this implies that pulsar timing arrays cannot constrain theories that only deviate significantly from GR in the late inspiral, while they are exceptionally well-suited for constraining low-frequency deviations.
Therefore, we see a complementarity emerging: different detectors can test GR in different complementary regimes:
- Ground-based detectors are best at constraining higher-curvature type modified theories that deviate from GR the most in the late inspiral and merger phase.
- Space-based detectors are best at constraining modified graviton dispersion relations and the geometry of supermassive compact objects.
- Pulsar-timing arrays are best at independently constraining the existence of both scalar modes and any deviation from GR that dominates at low orbital frequencies.
Through the simultaneous implementation of all these tests, GR can be put on a much firmer footing in all phases of the strong-field regime.
1.5 Notation and conventions
We mainly follow the notation of [318*], where Greek indices stand for spacetime coordinates and spatial
indices in the middle of the alphabet 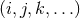 for spatial indices. Parenthesis and square brackets in
index lists stand for symmetrization and anti-symmetrization respectively, e.g.,
for spatial indices. Parenthesis and square brackets in
index lists stand for symmetrization and anti-symmetrization respectively, e.g., 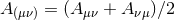 and
and ![A[μν] = (A μν − A νμ)∕2](article21x.gif) . Partial derivatives with respect to spacetime and spatial coordinates are
denoted
. Partial derivatives with respect to spacetime and spatial coordinates are
denoted 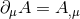 and
and 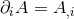 respectively. Covariant differentiation is denoted
respectively. Covariant differentiation is denoted 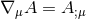 ,
multiple covariant derivatives
,
multiple covariant derivatives 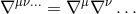 , and the curved spacetime D’Alembertian
, and the curved spacetime D’Alembertian
 . The determinant of the metric
. The determinant of the metric 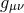 is
is 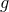 ,
, 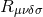 is the Riemann tensor,
is the Riemann tensor, 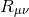 is
the Ricci tensor,
is
the Ricci tensor, 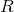 is the Ricci scalar and
is the Ricci scalar and 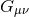 is the Einstein tensor. The Levi-Civita
tensor and symbol are
is the Einstein tensor. The Levi-Civita
tensor and symbol are 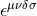 and
and 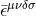 respectively, with
respectively, with 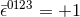 in an orthonormal,
positively-oriented frame. We use geometric units (
in an orthonormal,
positively-oriented frame. We use geometric units (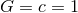 ) and the Einstein summation convention is
implied.
) and the Einstein summation convention is
implied.
We will mostly be concerned with metric theories, where gravitational radiation is only defined much farther than a gravitational-wave wavelength from the source. In this far or radiation zone, the metric tensor can be decomposed as
with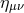 the Minkowski metric and
the Minkowski metric and 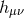 the metric perturbation. If the theory considered has additional
fields
the metric perturbation. If the theory considered has additional
fields 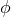 , these can also be decomposed in the far zone as
with
, these can also be decomposed in the far zone as
with 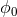 the background value of the field and
the background value of the field and 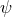 a perturbation. With such a decomposition, the field
equations for the metric will usually be wave equations for the metric perturbation and for the field
perturbation, in a suitable gauge.
a perturbation. With such a decomposition, the field
equations for the metric will usually be wave equations for the metric perturbation and for the field
perturbation, in a suitable gauge.