1 Introduction
For almost a century, the theory of general relativity (GR) has been known to describe the force of gravity with impeccable agreement with observations. Despite all the successes of GR the search for alternatives has been an ongoing challenge since its formulation. Far from a purely academic exercise, the existence of consistent alternatives to describe the theory of gravitation is actually essential to test the theory of GR. Furthermore, the open questions that remain behind the puzzles at the interface between gravity/cosmology and particle physics such as the hierarchy problem, the old cosmological constant problem and the origin of the late-time acceleration of the Universe have pushed the search for alternatives to GR.While it was not formulated in this language at the time, from a more modern particle physics perspective GR can be thought of as the unique theory of a massless spin-2 particle [287*, 483*, 175*, 225*, 76*], and so in order to find alternatives to GR one should break one of the underlying assumptions behind this uniqueness theorem. Breaking Lorentz invariance and the notion of spin along with it is probably the most straightforward since non-Lorentz invariant theories include a great amount of additional freedom. This possibility has been explored at length in the literature; see for instance [398] for a review. Nevertheless, Lorentz invariance is observationally well constrained by both particle and astrophysics. Another possibility is to maintain Lorentz invariance and the notion of spin that goes with it but to consider gravity as being the representation of a higher spin. This idea has also been explored; see for instance [466, 52] for further details. In this review, we shall explore yet another alternative: Maintaining the notion that gravity is propagated by a spin-2 particle but considering this particle to be massive. From the particle physics perspective, this extension seems most natural since we know that the particles carrier of the electroweak forces have to acquire a mass through the Higgs mechanism.
Giving a mass to a spin-2 (and spin-1) field is an old idea and in this review we shall summarize the approach of Fierz and Pauli, which dates back to 1939 [226]. While the theory of a massive spin-2 field is in principle simple to derive, complications arise when we include interactions between this spin-2 particle and other particles as should be the case if the spin-2 field is to describe the graviton.
At the linear level, the theory of a massless spin-2 field enjoys a linearized diffeomorphism (diff)
symmetry, just as a photon enjoys a 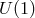 gauge symmetry. But unlike for a photon, coupling the spin-2
field with external matter forces this symmetry to be realized in a different way non-linearly. As a result,
GR is a fully non-linear theory, which enjoys non-linear diffeomorphism invariance (also known as general
covariance or coordinate invariance). Even though this symmetry is broken when dealing with a massive
spin-2 field, the non-linearities are inherited by the field. So, unlike a single isolated massive spin-2 field, a
theory of massive gravity is always fully non-linear (and as a consequence non-renormalizable) just as for
GR. The fully non-linear equivalent to GR for massive gravity has been a much more challenging theory to
obtain. In this review we will summarize a few different approaches to deriving consistent theories
of massive gravity and will focus on recent progress. See Ref. [309] for an earlier review on
massive gravity, as well as Refs. [134] and [336] for other reviews relating Galileons and massive
gravity.
gauge symmetry. But unlike for a photon, coupling the spin-2
field with external matter forces this symmetry to be realized in a different way non-linearly. As a result,
GR is a fully non-linear theory, which enjoys non-linear diffeomorphism invariance (also known as general
covariance or coordinate invariance). Even though this symmetry is broken when dealing with a massive
spin-2 field, the non-linearities are inherited by the field. So, unlike a single isolated massive spin-2 field, a
theory of massive gravity is always fully non-linear (and as a consequence non-renormalizable) just as for
GR. The fully non-linear equivalent to GR for massive gravity has been a much more challenging theory to
obtain. In this review we will summarize a few different approaches to deriving consistent theories
of massive gravity and will focus on recent progress. See Ref. [309] for an earlier review on
massive gravity, as well as Refs. [134] and [336] for other reviews relating Galileons and massive
gravity.
When dealing with a theory of massive gravity two elements have been known to be problematic since the seventies. First, a massive spin-2 field propagates five degrees of freedom no matter how small its mass. At first this seems to suggest that even in the massless limit, a theory of massive gravity could never resemble GR, i.e., a theory of a massless spin-2 field with only two propagating degrees of freedom. This subtlety is at the origin of the vDVZ discontinuity (van Dam–Veltman–Zakharov [465*, 497*]). The resolution behind that puzzle was provided by Vainshtein two years later and lies in the fact that the extra degree of freedom responsible for the vDVZ discontinuity gets screened by its own interactions, which dominate over the linear terms in the massless limit. This process is now relatively well understood [463*] (see also Ref. [35*] for a recent review). The Vainshtein mechanism also comes hand in hand with its own set of peculiarities like strong coupling and superluminalities, which we will discuss in this review.
A second element of concern in dealing with a theory of massive gravity is the realization that most non-linear extensions of Fierz–Pauli massive gravity are plagued with a ghost, now known as the Boulware–Deser (BD) ghost [75*]. The past decade has seen a revival of interest in massive gravity with the realization that this BD ghost could be avoided either in a model of soft massive gravity (not a single massive pole for the graviton but rather a resonance) as in the DGP (Dvali–Gabadadze–Porrati) model or its extensions [208*, 209*, 207*], or in a three-dimensional model of massive gravity as in ‘new massive gravity’ (NMG) [66*] or more recently in a specific ghost-free realization of massive gravity (also known as dRGT in the literature) [144*].
With these developments several new possibilities have become a reality:
- First, one can now more rigorously test massive gravity as an alternative to GR. We will
summarize the different phenomenologies of these models and their theoretical as well as
observational bounds through this review. Except in specific cases, the graviton mass is typically
bounded to be a few times the Hubble parameter today, that is
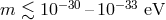 depending on the exact models. In all of these models, if the graviton had a mass much smaller
than
depending on the exact models. In all of these models, if the graviton had a mass much smaller
than 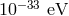 , its effect would be unseen in the observable Universe and such a mass would
thus be irrelevant. Fortunately there is still to date an open window of opportunity for the
graviton mass to be within an interesting range and providing potentially new observational
signatures.
, its effect would be unseen in the observable Universe and such a mass would
thus be irrelevant. Fortunately there is still to date an open window of opportunity for the
graviton mass to be within an interesting range and providing potentially new observational
signatures.
- Second, these developments have opened up the door for theories of interacting metrics, a success long awaited. Massive gravity was first shown to be expressible on an arbitrary reference metric in [296*]. It was then shown that the reference metric could have its own dynamics leading to the first consistent formulation of bi-gravity [293*]. In bi-gravity two metrics are interacting and the mass spectrum is that of a massless spin-2 field interacting with a massive spin-2 field. It can, therefore, be seen as the theory of general relativity interacting (fully non-linearly) with a massive spin-2 field. This is a remarkable new development in both field theory and gravity.
- The formulation of massive gravity and bi-gravity in the vielbein language were shown to be both analytic and much more natural and allowed for a general formulation of multi-gravity [314*] where an arbitrary number of spin-2 fields may interact together.
- Finally, still within the theoretical progress front, all of these successes provided full and definite proof for the absence of Boulware–Deser ghosts in these types of theories; see [295*], which has then been translated into a multitude of other languages. This also opens the door for new types of theories that can propagate fewer degrees than naively thought.
Independent of this, developments in massive gravity, bi-gravity and multi-gravity have also opened up new theoretical avenues, which we will summarize, and these remain very much an active area of progress. On the phenomenological front, a genuine task force has been devoted to finding both exact and approximate solutions in these types of gravitational theories, including the ones relevant for black holes and for cosmology. We shall summarize these in the review.
This review is organized as follows: We start by setting the formalism for massive and massless spin-1 and -2 fields in Section 2 and emphasize the Stückelberg language both for the Proca and the Fierz–Pauli fields. In Part I we then derive consistent theories using a higher-dimensional framework, either using a braneworld scenario à la DGP in Section 4, or via a discretization1 (or Kaluza–Klein reduction) of the extra dimension in Section 5. This second approach leads to the theory of ghost-free massive gravity (also known as dRGT) which we review in more depth in Part II. Its formulation is summarized in Section 6, before tackling other interesting aspects such as the fate of the BD ghost in Section 7, deriving its decoupling limit in Section 8, and various extensions in Section sec:Extensions. The Vainshtein mechanism and other related aspects are discussed in Section 10. The phenomenology of ghost-free massive gravity is then reviewed in Part III including a discussion of solar-system tests, gravitational waves, weak lensing, pulsars, black holes and cosmology. We then conclude with other related theories of massive gravity in Part IV, including new massive gravity, Lorentz breaking theories of massive gravity and non-local versions.
Notations and conventions:
Throughout this review, we work in units where the reduced Planck constant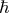 and the speed of light
and the speed of light
 are set to unity. The gravitational Newton constant
are set to unity. The gravitational Newton constant 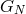 is related to the Planck scale by
is related to the Planck scale by
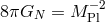 . Unless specified otherwise,
. Unless specified otherwise, 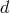 represents the number of spacetime dimensions. We use the
mainly
represents the number of spacetime dimensions. We use the
mainly  convention
convention  and space indices are denoted by
and space indices are denoted by 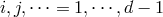 while
while 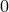 represents the time-like direction,
represents the time-like direction, 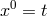 .
.
We also use the symmetric convention: 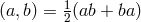 and
and ![[a,b] = 1(ab − ba) 2](article17x.gif) . Throughout this
review, square brackets of a tensor indicates the trace of tensor, for instance
. Throughout this
review, square brackets of a tensor indicates the trace of tensor, for instance ![μ [𝕏 ] = 𝕏 μ](article18x.gif) ,
, ![2 μ ν [𝕏 ] = 𝕏 ν𝕏 μ](article19x.gif) ,
etc…. We also use the notation
,
etc…. We also use the notation 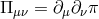 , and
, and 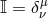 .
. 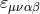 and
and 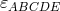 represent the
Levi-Cevita symbol in respectively four and five dimensions,
represent the
Levi-Cevita symbol in respectively four and five dimensions, 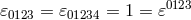 .
.

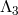 -decoupling
limit of bi-gravity
-decoupling
limit of bi-gravity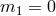
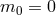 )
)