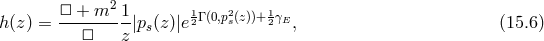15 Non-local massive gravity
The ghost-free theory of massive gravity proposed in Part II as well as the Lorentz-violating theories of Section 14 require an auxiliary metric. New massive gravity, on the other hand, can be formulated in a way that requires no mention of an auxiliary metric. Note however that all of these theories do break one copy of diffeomorphism invariance, and this occurs in bi-gravity as well and in the zwei dreibein extension of new massive gravity.One of the motivations of non-local theories of massive gravity is to formulate the theory without any reference metric.34 This is the main idea behind the non-local theory of massive gravity introduced in [328*].35
Starting with the linearized equation about flat space-time of the Fierz–Pauli theory
where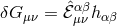 is the linearized Einstein tensor, this modified Einstein equation can be
‘covariantized’ so as to be valid about for any background metric. The linearized Einstein tensor
is the linearized Einstein tensor, this modified Einstein equation can be
‘covariantized’ so as to be valid about for any background metric. The linearized Einstein tensor
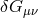 gets immediately covariantized to the full Einstein tensor
gets immediately covariantized to the full Einstein tensor 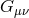 . The mass term, on
the other hand, is more subtle and involves non-local operators. Its covariantization can take
different forms, and the ones considered in the literature that do not involve a reference metric are
where
. The mass term, on
the other hand, is more subtle and involves non-local operators. Its covariantization can take
different forms, and the ones considered in the literature that do not involve a reference metric are
where 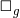 is the covariant d’Alembertian
is the covariant d’Alembertian 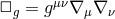 and
and 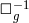 represents the retarded
propagator. One could also consider a linear combination of both possibilities. Furthermore, any of
these terms could also be implemented by additional terms that vanish on flat space, but one
should take great care in ensuring that they do not propagate additional degrees of freedom (and
ghosts).
represents the retarded
propagator. One could also consider a linear combination of both possibilities. Furthermore, any of
these terms could also be implemented by additional terms that vanish on flat space, but one
should take great care in ensuring that they do not propagate additional degrees of freedom (and
ghosts).
Following [328*] we use the notation where 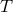 designates the transverse part of a tensor. For any tensor
designates the transverse part of a tensor. For any tensor
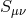 ,
,
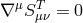 . In flat space we can infer the relation [328]
. In flat space we can infer the relation [328]
The theory propagates what looks like a ghost-like instability irrespectively of the exact formulation chosen in (15.2*). However, it was recently argued that the would-be ghost is not a radiative degree of freedom and therefore does not lead to any vacuum decay. It remains an open question of whether the would be ghost can be avoided in the full nonlinear theory.
The cosmology of this model was studied in [395, 228]. The new contribution (15.2*) in the Einstein
equation can play the role of dark energy. Taking the second formulation of (15.2*) and setting the
graviton mass to 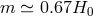 , where
, where 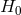 is the Hubble parameter today, reproduces the
observed amount of dark energy. The mass term acts as a dark fluid with effective time-dependent
equation of state
is the Hubble parameter today, reproduces the
observed amount of dark energy. The mass term acts as a dark fluid with effective time-dependent
equation of state 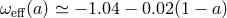 , where
, where  is the scale factor, and is thus
phantom-like.
is the scale factor, and is thus
phantom-like.
Since this theory is formulated at the level of the equations of motion and not at the level of the action and since it includes non-local operators it ought to be thought as an effective classical theory. These equations of motion should not be used to get some insight on the quantum nature of the theory nor on its quantum stability. New physics would kick in when quantum corrections ought to be taken into account. It remains an open question at the moment of how to embed nonlocal massive gravity into a consistent quantum effective field theory.
Notice, however, that an action principle was proposed in Ref. [402*], (focusing on four dimensions),
where the function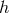 is defined as
where
is defined as
where 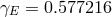 is the Euler’s constant,
is the Euler’s constant, 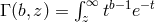 is the incomplete gamma function,
is the incomplete gamma function,
 is a integer
is a integer 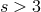 and
and 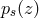 is a real polynomial of rank
is a real polynomial of rank  . Upon deriving the equations
of motion we recover the non-local massive gravity Einstein equation presented above [402],
up to order
. Upon deriving the equations
of motion we recover the non-local massive gravity Einstein equation presented above [402],
up to order 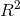 corrections. We point out however that in this action derivation principle the operator
corrections. We point out however that in this action derivation principle the operator
 likely correspond to a symmetrized Green’s function, while in (15.2*) causality requires
likely correspond to a symmetrized Green’s function, while in (15.2*) causality requires  to
represent the retarded one.
to
represent the retarded one.
We stress, however, that this theory should be considered as a classical theory uniquely and not be quantized. It is an interesting question of whether or not the ghost reappears when considering quantum fluctuations like the ones that seed any cosmological perturbations. We emphasize for instance that when dealing with any cosmological perturbations, these perturbations have a quantum origin and it is important to rely of a theory that can be quantized to describe them.

 -decoupling
limit of bi-gravity
-decoupling
limit of bi-gravity
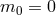 )
)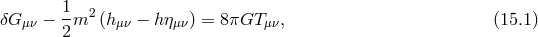
![{ ( −1 )T 1(hμν − hη μν) −→ □(g G μν ) Ref. [328] , (15.2 ) 2 38 gμν□ −g1R T Refs. [395, 229, 228]](article2831x.gif)

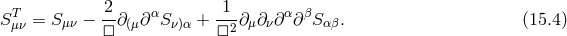
![∫ [ ] 4 √ --- M-2Pl ¯ M-2Pl- ( -□--) μν S = d x − g 2 R + λ + 2M 2R μνh − M 2 G , (15.5 )](article2844x.gif)