数学入門公開講座 バックナンバー(講義ノート)
令和7年8月4日-8月7日(第46回) 演題及び講師
数え上げ幾何学と導来代数幾何学
助教・金城 翼
平面上に三つの円が与えられたとき、その全てに接する円はいくつあるでしょうか?この問題はアポロニウスの問題と呼ばれ、2000年以上の歴史を持ちます。このような幾何学的な対象の数え上げを研究する数学領域を「数え上げ幾何学」と言います。数え上げ幾何学は素朴な出発点を持つ一方で、現代数学における様々な理論と関わり、現在でも活発に研究が行われています。特に、2000年ごろに登場した「導来代数幾何学」と呼ばれる代数幾何学の最新のフレームワークとの関連が近年注目を集めています。本講座ではまず27本の
直線などの古典的な数え上げ幾何学の問題を解説し、その後導来代数幾何学の哲学および数え上げ幾何学への応用を紹介します。
講演映像:
1日目
2日目
3日目
4日目
流体力学と数理科学諸分野との関わり
教授・大木谷 耕司
粘性流体のナビエストークス方程式を軸に、流体力学と数理科学諸分野との関係を垣間見る。
以下のものを含む話題を予定している。
1 )簡単な厳密解による、乱流理論でのエネルギー散逸率の重要性(流体物理)
2 )非粘性流体のオイラー方程式のハミルトン系としての定式化(微分幾何)
3 )シュレディンガー方程式と流体方程式との関連(量子力学)
4 )オンサーガー予想について最近の発展(微分幾何)
講演映像:
1日目
2日目
3日目
4日目
アフィン量子群の表現論入門
助教・藤田 遼
表現論は種々の代数系の線形空間への作用を通じて対称性を研究する分野です。表現論で扱う代数系として単純リー代数は古典的ですが、20世紀後半以降その「アフィン化」や「量子化」といった変種が物理学との関係もあって注目を浴び、現在も様々なトピックと結びつきながら研究の進展が続いています。この講座では単純リー代数の「アフィン化+量子化」にあたるアフィン量子群の表現論について入門的な解説を試みます。特に最も簡単な単純リー代数 sl2に付随する場合に表現を具体的に計算し、その表現論の面白さと最新の研究成果の一端に触れたいと思います。
講演映像:
1日目
2日目
3日目
4日目
◇特別講演◇
Web サービスを支える数学
LINE ヤフー研究所長 田島 玲
日々多くのユーザーの皆様に使っていただいている web サービスでは、裏側で数学に基づく技術が多く活用されています。本講演では、安心・安全と興味・関心という二つの視点を軸に、数学がどのように実社会のサービスを支えているのかを事例をもとに紹介します。まず、FIDO 認証などの暗号技術や連合学習・差分プライバシーを取り上げ、大規模なユーザーデータを扱う上で欠かせない安全性やプライバシー保護の工夫をご紹介します。また、ユーザーの興味やニーズに応えるために活用されるベクトル検索による高速な類似探索、統計的因果推論による施策効果の検証などについても取り上げ、数学がサービスの快適さやユーザー体験の向上にどのように応用されているかを例示します。
令和6年7月29日-8月1日(第45回) 演題及び講師
スペクトル不変量とその応用について
助教・石川 卓
大学で習う幾何学の基本的な話に Morse 理論というものがあります。これは多様体の性質を、その上の函 数を用いて調べる理論です。これは基本的にはどのような関数を用いても同じ答えを出しますが、これを逆 に利用して、各関数に対してスペクトル不変量とよばれる値を紐づけることができます。シンプレクティッ ク幾何学等で用いられる Floer 理論は Morse 理論を手本としてつくられた理論であり、これに対するスペク トル不変量が、幾何学的性質を導きだすことに応用されています。このあたりのことについて、紹介する予 定です。
体構造の復元を通した遠アーベル幾何学入門
助教・辻村 昇太
遠アーベル幾何学では(体に対するガロア群のような)構造の対称性のなす群が元の構造の情報をどの程 度保持しているかについて考察します。この対称性のなす群が(高度に)非可換/非アーベル的な設定を扱 うため、 「遠アーベル」と名付けられています。本講義では、体構造がその絶対ガロア群の純群論的構造から どの程度復元されるかという遠アーベル幾何学における基本的な問題を取り上げます。体の絶対ガロア群の ような基本的な概念を説明した後、数論的に興味深いいくつかの設定でどのようなことが知られているかに ついて解説する予定です。
シンプレクティック特異点と代数幾何
教授・並河 良典
代数幾何では特異点が重要な働きをしますが、この講演では、シンプレクティック特異点とよばれる対象 について紹介します。シンプレクティック特異点は、代数幾何や幾何学的表現論の様々な場面で登場します。 例えば、複素正方行列で何回か掛けると 0 になるようなもの全体を考えるとシンプレクティック特異点をもっ た代数多様体になります。また、トーリック超ケーラー多様体とよばれる代数多様体もこうした特異点を持 ちます。具体例をゆっくりと説明しながら、シンプレクティック特異点に関わるいくつかの話題にアプロー チしていく予定です。
◇特別講演◇
C* 環を用いたデータ解析
NTT ネットワークサービスシステム研究所特別研究員・橋本 悠香
C* 環は、複素数全体の集合を自然に拡張したもので、これまで複素数として考えられていた概念を関数や 作用素へ拡張することを可能とします。本講演では、C* 環のデータ解析への応用について述べます。近年、 データやそれを解析するためのモデルは複雑化しており、高精度な解析を行うためには、より多くの情報を データから抽出するための枠組みが必要となっています。そこで、C* 環を用いて既存のデータ解析手法を拡 張し、複雑なデータやモデルを解析することについて解説します。C* 環を用いた手法の理論的側面について も触れ、どこに難しさがあるのかについても述べます。
令和5年7月31日-8月3日(第44回) 演題及び講師
ヒッチン方程式とその周辺
教授・望月 拓郎
ヒッチン方程式はリーマン面上で定義される非線形な微分方程式です。もともとは物理学で重要なヤン - ミルズ方程式を簡単にしたものとして導入されたのですが、むしろ数学的に興味深い方程式であり、微分幾 何・代数幾何・トポロジーなど様々な分野を結びつける役割を果たし、その影響は代数解析や数論といった かなり離れた分野にまで及んでいます。この講座では、ヒッチン方程式に関連する数学的対象について説明 し、ヒッチン方程式に触発されて発展した研究の一端を紹介する予定です。また、ヒッチン方程式を例とし て、非線形微分方程式の解析の難しさと面白さなどについても触れたいと考えています。
二重指数関数型数値積分公式の理論と発展
助教・大浦 拓哉
二重指数関数型数値積分公式(DE 公式)は高橋秀俊・森正武により1974年に提案された定積分の値を数
値的に求める手法です。現在この DE 公式は様々な数学ソフトウェアに組み込まれており、理工系の分野で
広く利用されています。DE 公式の特徴は計算できる定積分の範囲が広いことから広義積分の計算にも適用
可能であること、また計算精度が任意にコントロールできるということです。古典的な数値積分公式にはな
いこれらの優れた特徴はコンピュータへの実装を容易にし、この公式を実用性に優れたものにしています。本
講義では、まず DE 公式の理論を解説し、その公式の普及と発展・応用についてご紹介したいと思います。
スライド:
1
2
3
4
代数トポロジーと物理学
特任准教授・山下 真由子
幾何学・トポロジーにおいて、図形や多様体などの幾何学的対象を分類するというのは基本的な問題であ
り、代数トポロジーとは、幾何学的対象の情報を扱いやすい代数的な情報に落として不変量を得る枠組みと
いえます。このように純粋数学的な問題意識から発展してきた代数トポロジーの手法が、近年物理学に応用
できることが明らかにされ、注目を集めています。本講義では、代数トポロジーを物理学の分類問題に応用
する基本的なアイデアを、物性物理学や素粒子物理学に現れる例に基づいて解説します。
講演映像:
1日目
2日目
3日目
4日目
◇特別講演◇
人流データの複雑ネットワーク分析とその応用
東北大学大学院情報科学研究科・藤原
直哉 准教授
人流データと呼ばれる、人々の移動に関するデータが近年利用可能となっており、様々な場面で応用され ています。人流データはいわゆるビッグデータの一種ですが、このような巨大なデータを取り扱う数理的な 手法が必要となっています。人流は地点間の関係を表すので地理空間におけるネットワークとして捉えるこ とが可能です。本講演では、複雑ネットワークに関する近年の発展について解説するとともに、応用例とし て、ネットワーク上における感染症の数理モデルを導入し、人流データを用いたネットワークにおける感染 症伝播に関する話題を紹介します。
令和4年8月1日-8月4日(第43回) 演題及び講師
フラクタル上のラプラシアン・熱方程式入門
准教授・梶野 直孝
空間内の領域を占めている均質な媒質における温度分布の経時変化が、「時間変数に関する 1 階偏微分が空間変数に関する 2 階偏微分の和(ラプラシアン)に等しい」という形の偏微分方程式(熱方程式)の解として記述できることはよく知られています。一方、確率論や統計物理学では「フラクタル」と呼ばれる、Euclid空間内の領域とは全く異なる幾何的性質を有する図形が様々な背景の下自然に現れ、そのような図形においてラプラシアンや熱方程式を厳密に定式化し解析することは近年の確率論研究の重要テーマとなっています。
本講義では、最も基本的なフラクタルである Sierpinski gasket を例に取り、その上のラプラシアン・熱方程式の厳密な定式化と基本性質について解説します。
講義の映像:
1日目
2日目
3日目
4日目
不変量で見るトポロジー
助教・石川 勝巳
与えられた 2 つの図形が同じものか判定せよというのは幾何学の基本的な問題の 1 つですが、何を以て「同じ」とするかは分野によって様々です。例えばトポロジーという分野では繋がり方が同じ図形は全て同じものとみなして考えるので、一見すると全く異なる図形が実は同じものだったというようなことが起こります。そのような状況で図形を調べるのに便利なのが、見かけの形に依らず変わらない値を取る「不変量」を用いるという考え方です。抜き出してきた本質的な情報から元の対象を調べるという意味でこのような考え方は数学の至るところに現れますが、今回は特に低次元トポロジーを題材に不変量の世界をご紹介したいと思います。
講義の映像:
1日目
2日目
3日目
4日目
日常を彩る流体力学:「ながれ」の数理モデル
准教授・石本 健太
決まった形を持たず、刻一刻と変化する流体の運動は、捉えどころない印象を持ちます。Euler 以降250年以上に渡り、人類は流体運動、そして流体方程式の見せる様々な表情を追いかけてきました。流体力学の枠組みは、水や空気といった古典的な対象だけでなく、今や生物や宇宙に至るまで、その領域を拡げています。
本講義では、身の回りの現象を例にとりながら、流体力学を数理モデルの観点から捉え直し、普段から目にしているにもかかわらず、「見えていなかった」流体力学の豊かな世界を紹介したいと思います。
講義の映像:
1日目
2日目
3日目
4日目
スライド:
1
2
3
4
◇特別講演◇
数理最適化による社会の課題解決
(株) NTT データ数理システム・藤井 浩一氏
機械学習やビッグデータ分析など、高度な数学が実社会に影響を与えることが増えてきました。数理最適化もそのような数学の一つです。歴史的には「オペレーションズ・リサーチ」という軍事的研究から生まれた数理最適化が、コンピュータの発展とともに、現代社会の課題解決には欠かせない数学となっていきました。本講演では、数理最適化の基本的な考え方やアルゴリズム手法を初等的に解説し、身近な問題の解決にどう活躍しているかについて紹介します。
2021年8月2日-8月5日(第42回) 演題及び講師
計算量理論入門 ——「複雑さ」をとらえる
准教授・河村 彰星
農具や機械が人に素手よりも大きな力を与えるように、計算機(コンピュータ)は人の頭脳(数学力)を拡張し、問題解決能力を著しく高めました。ではそれによって問題の難しさがだんだん気にならなくなるかというと、さにあらず。歴史的にはむしろ、人が数理的に扱える範囲が広がれば広がるほど、計算機の性能向上や計算手順の工夫では乗り越えられない本質的な複雑さというものが、ますます鮮明に見えてきました。本講義では、この「計算しにくさ」の尺度で様々な数学的対象の複雑度を測るという立場から、計算量理論の枢要な考え方とその適用例や未解決予想について解説します。
講義のスライド
https://www.kurims.kyoto-u.ac.jp/~kawamura/t/kokai/
Frobenius写像の周辺
助教・越川 皓永
素数pが0に等しいような代数では、数をp乗する操作がFrobenius写像とも呼ばれます。この場合が特別視されるのは、2つの数の和のp乗がp乗してから和を取ったものと等しくなるためです。Frobenius写像は例えば有限体のGalois理論を統制する役割を果たし、これはいわゆるWeil予想へと繋がっていきます。一方、pが0と等しくない状況でも、Frobenius写像の代わりにその「持ち上げ」を考えるということが昔からされてきました。最近の研究において、この「持ち上げ」が改めて注目されています。ここでは、このような視点に重点をおいて、有限体やWittベクトルといった事項をなるべく初等的に紹介したいと思います。
代数曲面の自己正則写像
准教授・中山 昇
代数曲面は2次元の“代数的に定義された図形”ですが, この話では2次元コンパクト複素解析的多様体で射影空間に埋め込まれるものを考えます。代数曲面 Xの自己正則写像とは、正則写像 f : X → Xのことですが、この話ではさらに f が全射 (つまり f(X) = X) であって、しかも同型写像でないものを扱います。このような自己正則写像をもつ代数曲面は特殊であり、ある種の対称性を持つものになります。この曲面が特異点を持たない場合の分類結果について解説します。またその準備として、一般の代数曲面の分類理論についても概説します。
2020年
コロナ禍のため中止となりました
2019年7月29日-8月1日(第41回) 演題及び講師
関数不等式とエネルギー集約
教授・中西 賢次
偏微分方程式は、物理法則などを空間や時間を変数とする関数とその微分を使って表したものですが、多くの方程式は等式変形で具体的に解くことはできず、その代わりに関数に対する不等式が数学的な解析の中心的役割を果たします。また、不等式が成り立つか成り立たないかギリギリの所を調べることで、対応する関数や方程式の解の性質が大きく変化する境目が見えてきますが、その臨界的状況ではしばしば、物理的にはエネルギーの集約と見なせる現象が現れます。この講義では、様々な関数不等式の導出とその臨界現象および方程式への応用について、簡単なものから最近の研究まで幾つかの話題を選んでお話ししたいと思います。
組合せ最適化における双対性
(スライド)
准教授・小林 佑輔
最適化問題とは、与えられた制約の下で何らかの目的関数を最大化もしくは最小化する問題のことをいいます。その中でも特に、扱う対象がグラフやネットワーク、マトロイドのような組合せ的な構造を持つ場合には組合せ最適化問題と呼ばれ、理論・応用の両面から盛んに研究されています。いくつかの組合せ最適化問題を解く(効率的なアルゴリズムを与える)際には、ある問題の最大値と全く別の問題の最小値が一致するという形の最大最小定理が重要な役割を果たします。このような一見無関係に見える二つの問題の関係は双対性と呼ばれ、アルゴリズムの設計に有用なだけではなく、理論的にも興味深いものとなっています。本講義では、組合せ最適化の中でも、特にグラフ上の最適化問題に注目し、そこに現れる双対性について紹介します。
流体力学 ---- まだこんなことが分からない
教授・山田 道夫
流体力学は古典力学の一分野として、18世紀のEulerの時代以来、今日まで300年近い長い歴史を持っています。また、それが対象とするものは、私たちに身近な水や空気であるため、隅々まで分かっているように思われるかもしれませんが、実は基本法則にも、あるいはそれが記述する流体の運動にも、理解を拒み続けている問題が潜んでいます。ここではそのような問題のいくつかを題材にして、古くて新しい流体力学を紹介したいと思います。
2018年7月30日-8月2日(第40回) 演題及び講師
代数幾何の源流を求めて 教授・向井 茂
代数幾何は、言葉の通り、代数を用いて幾何(あるいはその逆)を研究する。よって、デカルト的な座標幾何は当然の前提としている。しかし、座標系に依存しない概念や道具がなければ闇雲な計算の集まりに堕してしまう。その点でポンスレー等による射影幾何学の基礎付けには、無限遠点の導入(コンパクト化)や双対平面(モジュライの元祖)のように、現代数学に欠かせないアイデアも含まれていて、代数幾何の一つの由緒正しい源であると言えるだろう。講演では、この辺りを復習した後、6角形や3角形対に対する古典的定理群(パッポス、パスカル、デザルグ等)を代数幾何的に紹介する。また、これらに関係する現代的話題を、最近の進展が著しいクレモナ群の研究などから紹介したい。
シンプレクティック双対性入門 助教・疋田 辰之
幾何学的表現論と呼ばれる分野では表現論をある種の良い性質を持つ空間の幾何を用いて研究します。最近では半単純リー代数の表現論の一般化として、シンプレクティック特異点解消と呼ばれる性質を持つ多様体とそれにまつわる表現論が研究されています。そしてシンプレクティック双対性とは、あ る意味で半単純リー代数のラングランズ双対の一般化と見なせるシンプレクティック特異点解消の間の双対性です。この双対性についてはまだ分かっていないことが多いですが、双対であると考えられるシンプレクティック特異点解消の間には様々な不思議な関係があることが観察されています。講義ではそのような現象の一端をできるだけ簡単な例で紹介したいと思います。
「代数学入門」入門としての普遍代数学 准教授・照井 一成
代数学の基礎事実の中には、群・環といった特定の代数構造にあまり依存しないものがあります。準同型定理がその典型例です。一方で、群・環の直積はやっぱり群・環ですが、体についてはそうはなりません。では、既知の性質や構成法は、どのような条件の下でどのような方向に一般化することができるのでしょうか?それを探求するのが普遍代数学です。
もちろん一般化すればするほどあまり面白いことはいえなくなっていくのですが、それでも一般化によって見えてくるものはありますし、代数各論を系統的に理解するためにも役に立ちます。本講義では予備知識を仮定せず、また特定の代数構造も仮定せず、「代数一般について何がどこまでいえるのか」をはじめから考えていきたいと思います。
2017年7月31日-8月3日(第39回) 演題及び講師
素数定理とRiemannゼータ関数 講師・山下 剛
素数とは、1と自分自身の2つ以外に約数をもたない自然数である。古代ギリシャでは素数が無限に存在することが知られていたが、古来より素数がどのように分布しているのか人類の大きな関心の1つである。Gauss自身の回想によると、与えられた自然数 N 以下に存在する素数の個数π(N )をたくさん計算することで1792年頃に
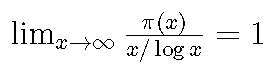
超準解析入門 -超実数と無限大の数学- 特定助教・磯野 優介
「無限に大きい数」は存在しません。どんな数を持ってきても、それに1を足せば、より大きな数が出来るからです。同様に「無限に小さい数」も存在しません。このような無限数は、数学的に厳密に定義出来ないにもかかわらず、古くから研究に用いられてきました(いわゆる「無限小解析」)。その後19世紀に入り、厳密さを備えたε-δ論法が登場し、無限小解析は歴史から姿を消します。 超準解析とは、「無限に大きい、小さい数」を、数学として厳密に定式化し、取り扱う学問です。この枠組みでは、無限数を用いた計算や証明が可能で、現代数学を用いた無限小解析の再現とも言えます。この講義では、そのような無限数を含む「超実数」を構成し、それを用いて解析学の基礎的な定理を実際に証明してみようと思います。
五重積公式のADE一般化 -場の理論の視点から- (スライド) 准教授・河合 俊哉
有名なヤコビの三重積公式に似たワトソンの五重積公式と呼ばれる古典的な恒等式があります。この公式のある種の拡張(ADE一般化)が場の理論の視点から自然に導かれることを紹介したいと思います。使う場の理論は二次元のN=2超共形場理論というもので、これに付随した楕円種数と呼ばれる量の考察が鍵になります。二次元共形場理論はそれ自身で学習を要する分野ですので、講義では詳細に立ち入れないところも多々あると予想しますが、物理的考察が意図せず他の数学に貢献できる場合があるという事例の雰囲気を出来るだけ伝えたいと思います。
2016年8月1日-8月4日(第38回) 演題及び講師
結び目の数学 スライド: 1 2 3 4 特任助教・鈴木 咲衣
ひもを結ぶと結び目ができます。靴ひもの蝶ちょ結び、荷造りのひもの堅結び、ひもで綺麗な模様を形作る装飾品など、結び目は日常生活でもしばしば現れるとても身近な存在です。そんな結び目の研究が近年、数学の一分野として急速に発展しています。「結び目で数学?何をするの?」と思うかもしれません。でも、数学は自由。数や多項式だけではなく、結び目でも数学ができます。この講義では、結び目の数学を基礎からゆっくりお話し、結び目の不変量であるジョーンズ多項式を計算します。
プログラミング言語の意味論と圏論 教授・長谷川 真人
プログラミング言語の意味論(プログラム意味論)は、プログラムの構造を数学的に定式化・抽象化することによってコンピュータソフトウェアに関する諸問題を解決することを目的とする、コンピュータサイエンスの一分野です。そこでは、抽象的な現代数学の象徴とも言われる圏論が活発に応用されてきており、今や圏論抜きにプログラム意味論を語ることは困難といっても過言ではありません。
この講義では、圏論を用いたプログラム意味論の概要を紹介しつつ、そもそもプログラム意味論に求められる数学とはどのようなものなのか、なぜ圏論なのか、という素朴な疑問に、私なりに答えてみたいと思います。
微分方程式を解く 講師・岸本 展
微分方程式は様々な自然現象を理解するための基本的な道具であり、数学に限らず多くの分野における重要な研究対象です。一方で、特に非線形偏微分方程式については、中学・高校で学習する2次方程式のような解の公式がなく、具体的な解の表示はおろか解が存在するかどうかさえ簡単な問題ではありません。例えば、空気や水といった流体の運動を記述するNavier-Stokes方程式は私達にとって最も身近な非線形偏微分方程式の一つですが、この方程式に“良い性質を持った”解がいつでも存在するかどうかは途方もなく難しい問題で、Clay数学研究所によるミレニアム懸賞問題の一つとなっています。この講義では、微分方程式を構成する関数や微分といった基本的な事柄について触れつつ、最終的には簡単な非線形偏微分方程式を、関数解析的手法により実際に“解いて”みたいと思います。
2015年8月3日-8月6日(第37回) 演題及び講師
ポアンカレ予想とリッチフロー 助教・横田 巧
ポアンカレ予想とは「任意の単連結な3次元閉多様体は3次元球面に同相であろう」という1904年の H. Poincaré による位相幾何学(トポロジー)の予想で、2002~03年に G. Perelman がその証明を発表しました。実際には彼はポアンカレ予想を含む W. Thurston の幾何化予想を証明し、その証明には R. Hamilton が開発した(手術付き)リッチフローと、リーマン多様体の崩壊理論という微分幾何学の手法が使われています。彼の証明は多くの数学者達によって検証され、また今も沢山の研究を触発し続けています。
この講義では、ポアンカレ予想の意味やその解決にまつわるドラマよりも、その証明の数学的な中身に踏み込み、受講者にその雰囲気が少しでも伝わるような解説を試みたいと思います。
天体ダイナモ理論の数理 -- なぜ星や惑星は固有の磁場を持っているのか?
准教授・竹広 真一
地球を始めとする数々の天体、たとえば太陽などの星や木星などの惑星は固有の磁場を伴っています。このような磁場は天体内部の電気電導性物質が流れることによって生じる「ダイナモ作用」により生成・維持されていると考えられており、その数理モデルが古くは20世紀初めから研究されてきています。本講義では、ダイナモ作用の基本的な性質の解説から始めて、ダイナモ理論の歴史をたどり、最後に近年可能となったコンピュータシミュレーション計算による研究を紹介しようと思います。
バナッハ=タルスキーのパラドックス 教授・小澤 登高
バナッハ=タルスキーのパラドックスは、球体を3次元空間内で幾つかに分割し、それらを回転や平行移動させてうまく組み合わせることによって、元の大きさの球体を2つ作ることが出来るという定理である。これは、1≠1+1と矛盾するようにも見えるが、分割したパーツに体積がきちんと定義できないゆえに起こりうる現象である。(また、各パーツを動かす時に他のパーツをすり抜けることが出来るものとしている。)従って純理論的にはパラドックスではなく、歴とした定理である。この公開講座では、体積や面積とは何かという話題から始めて、バナッハ=タルスキーの定理の紹介(証明)をしたい。
2014年8月4日-8月7日(第36回) 演題及び講師
乗法的情報による加法構造の復元 講師・星 裕一郎
数や式に対するもっとも基本的な操作として、「加法(=足し算)」と「乗法(=掛け算)」があります。この加法・乗法という2つの操作は、非常に複雑に絡み合っており、例えば整数に関わる様々な問題の難しさは、ある意味において、この複雑な絡み合いに起因していると考えられます。一方、この絡み合いの1つの表れとして、数や式の適当な集まりに対して、そこで定義される加法を、その乗法的な情報によって記述・復元することができる場合があります。本講義では、そのようなタイプの数学的命題について、お話をしようと思います。
ビリヤードからシンプレクティック・トポロジーへ 助教・入江 慶
解析力学のハミルトンによる定式化では、位置と運動量を組にして相空間というものを考えます。相空間の幾何、特にその大域的な性質を調べる分野をシンプレクティック・トポロジーといって、近年盛んに研究されています。ハミルトン力学系の周期軌道の研究はその起源のひとつで、現在でもこの分野の重要な主題です。
講演の前半では、例としてビリヤード球の運動における周期軌道について考察し、バーコフによる古典的な定理を紹介します。この定理にはすでにシンプレクティック・トポロジーの一端が表れており、後半はそれを手掛かりに、より現代的な話題に進みたいと思います。
楽して計算するには -アルゴリズムの設計と解析 准教授・牧野 和久
近年の情報化社会において、高速なアルゴリズムを設計することは極めて重要である。しかしながら、P vs NP問題に代表されるように、与えられた問題が効率的に解けるができるかどうかは、容易には分からない現状にある。
本講義では、計算可能性,P,NPなどの計算量理論の基礎的な概念を説明すると同時に、高速アルゴリズム設計の意義や重要性を応用などを交えて議論する。その後、分割統治法や動的計画法などの高速なアルゴリズム設計のための手法およびその解析法を具体的な問題を用いて紹介する。
それ以外にも、NP困難な問題に対する最適化の手法を用いた近似アルゴリズムの設計法も議論する。
2013年8月5日-8月8日(第35回) 演題及び講師
型無しラムダ計算とモデル 助教・星野 直彦
ラムダ計算は数学で日常的に行われる関数抽象や関数適用など関数についての操作を形式化したもので、関数型プログラミング言語の基礎理論として研究されています。またラムダ計算はCurry-Howard同型と呼ばれる対応によって論理学と強く結び付いている研究対象でもあります。論理学の研究に直観主義論理、二階論理、古典論理、線型論理など多くの論理体系が現れるのと同様にラムダ計算の研究には単純型付きラムダ計算、多相型ラムダ計算、ラムダミュウ計算、線型ラムダ計算と多様なラムダ計算が現れます。この講義ではその中で最もシンプルな型無しラムダ計算を扱います。型無しラムダ計算は関数抽象と関数適用のみを純粋に形式化した体系ですが、型の概念が無いために我々の直観が働かない「関数」が型無しラムダ計算の世界では定義できます。そのために型無しラムダ計算の数学的モデルの構成が容易でないなどの問題があり古くから多くの研究がなされてきました。この講義では型無しラムダ計算が型を持たないために起こる現象について他のラムダ計算との比較も交えつつ解説します。
クラッシュアイスの数理 講師・福島 竜輝
液体に氷を入れて冷やすときに、同じ量の氷ならば砕いた方が冷却効率が良くなることは誰もが経験則として知っていることでしょう。しかし、なぜ/どれくらい、良くなるのでしょうか? 例えばもっともらしい仮説として「砕くと表面積が増えるから」ということが考えられますが、この仮説が正しいかどうかは数学的にはモデルを作って検証する必要があります。熱伝導はいわゆる熱方程式によって記述されると仮定し、氷は考えている領域のある部分の温度を0に保つ境界条件と考えるのが自然です。
本講義ではこのような設定のもとで冷却効率が境界条件付きLaplace作用素の固有値で表現されることを説明し、さらにそれが氷を砕いたときにどのような振る舞いを示すかをお話しします。
Morse理論とFloer理論 教授・小野 薫
空間をその上の関数を用いて調べることはよく行われる。中でも Morse理論と呼ばれる方法や考え方は、多くの重要な結果を導き、発展した。今回はそのような話題からいくつか取り上げる予定である。簡単な例を通して関数とその臨界点の説明をし、臨界点の存在が空間の性質とどう関わるのかを見ることから始め、Morse理論の考え方を説明する。
最後には、Morse理論の類似である周期的Hamilton系に対するFloer理論について紹介したい。
2012年7月30日-8月2日(第34回) 演題及び講師
無限の対称性をめぐって 荒川 知幸
有限次元単純リー環はディンキン図形によって分類されますが、その自然な拡張 としてKac-Moody代数と呼ばれる無限次元リー環があります。またこの仲間とし て、ビラゾロ代数や、もっと単純なハイセンベルグ代数などもあります。さらに 無限次元リー環の一般化として頂点代数と呼ばれる代数系も知られています。 無限次元リー環やその仲間たちが数学に登場したのは約50年ほど前で、長い数 学の歴史の中ではつい最近の出来事なのですが、今ではこれらは数学のさまざま な分野に登場しています。この講義では無限次元リー環やその仲間たちを紹介 し、その魅力について説明したいと思います。
グラフの剛性とマトロイド 谷川 眞一
伸び縮みしないm本の棒部材とn個のジョイントで構成された平面トラス構造が剛
であるためにはm≧2n‐3が必要であります。この条件はJ.C.Maxwellの時代から知
られている古典的な事実であり、構造物の剛性がそのグラフ構造(棒とジョイン
トの接続関係)に大きく依存している事を示唆しています。実際、殆ど全ての
ジョイント配置において平面トラス構造の剛性は対応するグラフ上の組合せ的性
質によって特徴付け可能な事がMaxwellの結果から約100年後の1970年にLamanに
よって証明されています。Lamanの定理自体は線形代数の基礎知識と単純なグラ
フ理論の議論で証明可能ですが、なぜそのような特徴付けが可能かを理解するた
めには、組合せ論・最適化分野に現れるマトロイドや劣モジュラ関数の理論が必
要となります。
本講義ではグラフの剛性問題を話題の中心として、情景解析やCADなど離散幾
何学の幾つかの問題に共通に現れるマトロイドを紹介し、各問題における組合せ
的特徴付け定理について解説したいと考えています。
数体と位相曲面に共通する「二次元の群論的幾何」 望月 新一
有理数体Qのような「数体」と、複数のドーナツの表面を合体させたような形 をしたコンパクトな「位相曲面」は一見して全く異質な数学的対象であり、初等 的な可換環論、つまり、「加減乗除」が可能な数学的対象としての構造の理論か ら見ても直接的に関連付けることは難しい。しかし数体の拡大体の対称性を記述 する「絶対ガロア群」と、コンパクトな位相曲面の有限次の被覆の対称性を統制 する「副有限基本群」を通して両者を改めて眺めてみると、「二次元的な群論的 絡まり合い」という形で大変に興味深い構造的な類似性が浮かび上がってくる。 本講義では様々な側面におけるこの種の類似性に焦点を当てながら、数体と位相 曲面の基礎的な理論について解説する。
2011年8月1日-8月4日(第33回) 演題及び講師
マルコフ連鎖と混合時間 ーカード・シャッフルの数理ー 熊谷 隆
トランプをするとき、ゲームの前にカードがしっかり混ざるようにカードを切り(シャッフルし)ますが、何回くらい切ればカードがよく混ざってくれるでしょうか?この問題は、一般にマルコフ連鎖が定常分布に近づくのにかかる時間(混合時間)を調べる問題として設定することができます。このような定式化の下、トランプを大体7回切ればよく、しかも7回前後で急に「よく混ざった」状態になることが、今から20年ほど前にP. Diaconis教授らによって証明されました。
この講義では、カード・シャッフルなどの具体例を念頭に置きながら、マルコフ連鎖とその混合時間について解説します。「急によく混ざった状態になる」という現象(cut-off現象)についても定式化し、具体例を通じてどのようなときにこの現象が起こるかについても触れたいと思います。
微分方程式の不確定特異点 望月 拓郎
方程式を理解するための一つの指針は、与えられた方程式を簡単なものに変換することでした。 例えば、連立一次方程式は行列に関するなじみ深い操作で簡単な形のものに変形することによって理解できました。
この講座で興味を持つ題材は、複素領域上の「可積分な線形微分方程式系」です。特に方程式の特異点のまわりにおける性質、いわゆる局所的性質に興味を持ちます。より粗い言い方をすると、特異点のまわりでどのぐらい簡単な形に変換できるか、が問題です。一変数の場合には、福原満洲雄を含む先人達による古典的な研究があり、確定特異点という比較的易しい特異点の場合にはモノドロミーによって分類されること、より難しい不確定特異点の場合にはモノドロミーとストークス構造によって分類されること、などが知られていました。多変数の場合にどうかを問うのは自然です。確定特異点の場合には一変数の場合とほぼ同様であることが以前から知られていました。一方、多変数の場合の不確定特異点の研究は最近になって進展があり、代数幾何におけるブローアップとよばれる操作を組み合わせることで、比較的簡単な形に変換できることが示されました。この講座では、一変数の古典的な話の復習から始めて、最近の発展までを概説したいと考えています。
特異点解消入門 川ノ上 帆
爆発と呼ばれる操作を繰り返すことにより代数多様体を非特異なものに取り替えることを特異点解消といいます。廣中平祐先生は1960年代に標数0の場合に特異点解消がいつでも可能であることを証明し、フィールズ賞を受賞されました。今や特異点解消は標数0の代数幾何学において基本的かつ必要不可欠な道具となっています。
廣中先生の証明は「廣中の電話帳」と呼ばれ長大さと難解さで夙に有名でしたが、近年の研究により大幅に簡易化されました。本講義では、超曲面の場合について特異点解消の証明を紹介します。時間が許せば正標数の場合の最近の進展についても簡単に紹介します。
2010年8月2日-8月5日(第32回) 演題及び講師
グラフ理論から組合せ最適化へ 岩田 覚
ケーニヒスベルグの七つの橋を一回ずつ通る周遊路を求める問題が、オイラーの一筆書き定理によって否定的に解決され、グラフ理論の端緒となったことはよく知られています。それでは、全ての橋を少なくとも一回ずつ通って元の点に戻る周遊路のうちで、長さが最短のものを見つけるにはどうしたらよいでしょうか? このような問題設定は、20世紀の半ばになって提起され、線形不等式系の理論を援用した効率的な解法が与えられました。
本講義では、この解法を中心に、グラフ上の最適化問題と多面体の整数性、アルゴリズムの計算量と良い特徴付けについて、解説します。
自然現象を数理的に理解する --自己組織化現象の数理解析-- 上田 肇一
自然界には、砂丘の風紋、雪の結晶、魚の模様など様々な美しい模様が存在し、そのような模様には規則的に見える幾何学的なパターンが存在します。そのようなパターンは、あらかじめ設計図が与えられているのではなく、粒子や分子などの個々の要素が、基本的な物理法則に従って運動することで模様を作ることから、自己組織化パターンと呼ばれています。自己組織化パターンは見た目に美しいという魅力に加えて、生命活動において重要な役割をしていることが知られており、現在、数学を含む様々な分野で盛んに研究されています。
本講座では、自然現象を数学的に理解することを目的として、フラクタルや分岐理論といった数学的概念を、結晶成長や動物の模様などの身近な自己組織化パターンを例に、計算機シミュレーションと演習問題を用いながら説明します。また、計算機を用いて自己組織化パターンを再現する方法にも簡単に触れます。
極小モデル理論の発展 川北 真之
代数幾何学の扱う対象は、代数多様体と呼ばれる、連立多項式の共通零点集合として定義される図形です。極小モデル理論とは、変数変換で写り合う代数多様体たちを本質的に同じものと捉え、各々の中から代表的な代数多様体を抽出する理論です。抽出の過程で多様体上の余計な曲線を収縮させるのですが、収縮によって悪い特異点を持つ多様体が生じます。それを回復させる操作がフリップと呼ばれる変換で、極小モデル理論において中心的な役割を果たします。3次元極小モデル理論は森によるフリップの存在を中心として90年代に完成しましたが、その高次元化は暫く模索段階でした。ところが2006年、ビルカー、カッシーニ、ヘイコン、マッカーナンは一般次元のフリップの存在を証明し、極小モデル理論は大きな前進を遂げました。講座では、このような極小モデル理論の最近の発展を、わかりやすく紹介します。
2009年7月30日-8月2日(第31回)
ディンキン図式をめぐって -- 数学におけるプラトン哲学 中島 啓
紀元前の哲学者プラトンは、正多面体が5種類しかないことを宇宙の基本原理としたそうです。現代数学のいろいろな分野に、この正多面体がディンキン図形として現れています。一次分数変換のなす有限群、リー環の分類、単純特異点の分類、箙の直既約表現の分類などがその例です。そして、これらの間にすぐには分からないが、隠された深い関係があることが次第に明かにされつつあります。これを数学におけるプラトン哲学と呼んでいます。この講義では、小学生にも分かると思われるクラスター代数の例から始めて、線形代数を知っていれば分かると思われる箙の表現論を紹介し、プラトン哲学を少し味わっていただこうと思っています。
『数学』を数学的に考える 照井 一成
数学にはいったい何ができて何ができないのだろうか。その可能性と限界を知りたい。そのために数学者の行う活動(定理を証明したり、反例を考案したり)を数学的に分析するのがメタ数学、ないしは数学基礎論と呼ばれる分野である。
本講義では、当分野における古典的な成果であるゲーデルの不完全性定理とその周辺について概説する。それが示唆するのは数学の本質的な限界であると同時に開かれた可能性であり、確固たる土台の非存在であると同時に諸理論が織りなす空間の豊饒さである。
方針としては算術階層に重点をおき、不完全性やさまざまな決定不能問題をその中に位置づけていく形で、統一的な解説を行う予定である。
多品種流の話 平井 広志
身のまわりには、様々なネットワークがあり、そして、その中に水や電気などの「もの」が流れています。 ネットワーク中の入り口から出口まで、どれだけたくさんの「もの」を流すことが出来るでしょうか?
これに答えるのがFord-Fulkersonによる最大流最小カット定理です。最大流最小カット定理は、組合せ最適化の分野における最も基本的な「双対定理」の1つです。
さて、ネットワーク中に互いに交じり合うことが出来ない、例えば水と油のような、複数の「もの」が流れている状況を考えましょう。これを取り扱うのが多品種流の理論です。 本講座では、最大流最小カット定理の多品種流への様々な拡張を紹介しながら、組合せ最適化における双対定理の考え方を学びたいと思います。
2008年8月4日-8月7日(第30回)
シューベルト計算入門 阿部 健
代数幾何の研究対象に「モジュライ」があります。「モジュライ」とは、然るべき幾何学的対象をパラメトライズするパラメータ空間のことです。曲線のモジュライ、射のモジュライ、ベクトル束のモジュライ、などいろいろなモジュライがあります。モジュライの構造を調べることによって、それがパラメトライズする幾何学的対象の性質が分かる、といったことがよくあります。
この講義では、直線や平面をパラメトライズするモジュライであるグラスマン多様体を扱います。「3次元空間内に配置された4本の直線全てと交わる直線は何本?」という様な、直線や平面の数え上げ問題を解けるようになることを目標にして、グラスマン多様体上の交点数の計算方法であるシューベルト計算を紹介したいと思います。
関数の歴史 岡本 久
関数は現在数学の中心にある概念であり、これを用いずに理論を展開できる数学の分野はあまりないし、あったとしてもそれほど面白いものとはならないだろう。それくらい重要な概念であるが、その歴史的発展について講義などで語られることは少ない。昨今の大学では、 最も重要な知識だけをできるだけ短時間に教育することが最優先されていることが多く、 数学の発展過程において天才数学者たちがいかに右往左往したか、 ということにふれている余裕がなくなっている。
本講義の目的は、 数学といえどもその発展には多くの挫折が伴っていることを例示することにある。 そして我々の知っている関数がどうして今の位置を占めるようなってきたのかを具体例を使って説明したい。
量子古典対応とミクロ・マクロ双対性 小嶋 泉
マクロの可視的世界の下に目に見えない広大なミクロ世界が広がっていることは、エレクトロニクスはじめ、その原理・法則を応用した工業技術の恩恵に日夜浴する現代社会の「常識」だが、粒子性と波動性を併せ持つ電子・光子,原子・原子核・素粒子が飛び交い「不確定性原理」が支配する魑魅魍魎世界に隠された豊かな含意は十分正確には伝わっていない:数学の言葉でなら容易に記述・了解可能な量子世界の本質が、日常言語で表現できないという障壁のために。他方、その奇妙なミクロ量子世界と既知のマクロ古典世界とがどうつながっているか?は重要な問題のはずなのに殆ど議論されることがない。この講義では、後者を考える視点が前者の扱いにも有効な役割を果たすことを見たい。
2007年7月30日-8月2日(第29回)
解けない微分方程式をめぐって 竹井 義次
解析学の創始以来、微分方程式を解くことは解析学の中心課題の一つでした。常微分方程式に対する種々の解法の整備と Cauchy-Kowalevskyの定理等を背景として、1950年代頃まで少なくとも線形の微分方程式は局所的には解けるものと信じられていたようですが、 1957年に H. Lewyが解を持たない線形偏微分方程式を発見して状況は一変し、その後超局所解析の導入と相まって線形微分方程式に対する理解は急速に深まりました。
この講義では、微分方程式が解けるかどうかについて、いくつかの例を題材として、実領域と複素領域での可解性の相違や微分方程式とその背後に存在するある種の幾何学との関わりに触れながら論じてみたいと思います。
R = T 定理の仕組みとその応用 安田 正大
TaylorとWilesは、谷山-志村予想を解決するために R = T 定理の基本的手法を確立し、それを用いてWiles は Fermatの最終定理を証明しました。 R = T 定理の背後には Galois群と保型形式とを結びつけるLanglandsの哲学があります。4回の講義は各回とも前半と後半とに分かれます。 講義の前半では、R = T 定理の仕組み、定理の背景となる Langlandsの哲学、Fermatの最終定理その他への R = T 定理の応用について、最先端の話題を織り混ぜながらお話しします。講義の後半では、前半で用いられる数学を理解するための第一歩となる基本的な概念について、参加者のみなさんに慣れ親しんでもらい、さらに理解を深めるための方法をいくつかご提案したいと思います。
プログラミング言語の意味論 勝股 審也
プログラミング言語の意味論とは、広い意味では文字列であるプログラムに何らかの「意味」を対応させる事である。普段、私たちはプログラムに対しコンパイラやインタプリタによって機械語や計算機の振舞いを対応づけ、それらを実際の計算機で動かすことで実用的な恩恵を受けている。
一方、プログラミング言語の理論的な研究においては、プログラムに対してその挙動を表現するような数学的な対象や構造を対応させ、それらを数学的な道具や知識を援用して分析することで、プログラムや言語の性質を調べるということをする。この対応づけを研究する分野を(狭い意味での)プログラミング言語の意味論と言い、これが私の講義のトピックである。
意味論には様々なスタイルがあるが、今回は二通りの意味論を紹介する。一つは操作的意味論と呼ばれ、計算機の上でインタプリタを実装するのに似た自然な意味論である。もう一つは表示的意味論と呼ばれ、プログラムに対しその入出力関係を表現する関数を対応させる意味論である。この二つの意味論の間には「観測可能な範囲においてプログラムに同じ意味を与える」という、 adequacyと呼ばれる関係が成り立つ。本公開講座はこのadequacyを目指して講義を進めたい。
2006年7月31日-8月3日 (第28回)
ベクトル解析、微分方程式、流体力学 大木谷 耕司
流体力学では「場」を取り扱うため、その記述は偏微分方程式によってなされます。 講義では、流体力学の問題を論じる際に必要な数理的な道具を復習し、 1次元のモデル方程式などへの適用例を具体的に紹介します。 偏微分方程式のベクトル表示、熱拡散方程式の解法などから始めて、 モデル方程式の解析・計算例へと進みます。 最先端の課題や、数値解析的な手法にも触れる予定です。
クンツ環の話 阿部 光雄
n次複素正方行列においてS*S=I (S*はSの随伴行列、Iは単位行列)が成り立てば、 S*はSの逆行列(すなわち、Sはユニタリ行列)となり、 SS*=Iも成り立ちます。この結果の導出で重要なのは行列の有限次元性であり、 無限次元ではS*S=IとSS*=Iは必ずしも両立するとは限りません。例えば、 S*S=T*T=I, SS*+TT*=Iを満たす行列は有限次元では表すことが出来ません。 クンツ環とは、このような関係式を満たす2個以上の等長作用素 (S*S=Iを満たす作用素)で生成されるC*環のことです。ここで、 一般に複素数体上の環で、 複素行列の随伴行列を取ることを抽象化した*(スター)演算で閉じているものを *環と呼び、更にある特別な性質をもつノルム(C*ノルム)について完備なものを C*環と呼びます。この講義では、 *環としての代数的な側面からクンツ環が持ついくつかの興味深い性質について紹介したいと思います。
ガロア理論とその発展 玉川 安騎男
ガロア理論とは、Evariste Galois (1811-1832) によって創始された、 代数方程式の解の置換に関する理論です。 その基本定理は「体」と「群」という代数学の基本概念を用いて述べることができ、 現在でも整数論の研究の中で最も基本的な道具の1つであり続けています。 この講義では、まず、 ガロア理論の基本定理の感じをつかんでもらうことを目標にしたいと思います。 次に、 ガロア理論の古典的に有名な応用(ギリシャ数学3大難問のうちの角の3等分問題と立方体倍積問題の否定的解決、 あるいは、5次以上の方程式の加減乗除とべき根のみを用いた解の公式の非存在の証明、 など)の中から題材を選んで解説したいと思います。最後に、 遠アーベル幾何など、現代の整数論・数論幾何におけるガロア理論の展開についても紹介したいと思います。
2005年8月1日-8月4日(第27回)
3次元多様体のトポロジー 葉廣 和夫
多様体とは、局所的にユークリッド空間であるような図形です。 トポロジー(位相幾何学)では、 連続的な写像で一対一の対応がつく2つの図形を「位相同型」であるといい、 同等なものとみなします。 1次元、2次元の多様体の位相同型については、よくわかっていますが、 3次元多様体についてはまだ完全にはわかっていません。 この講義では、3次元多様体の位相同型類たちのなす集合の構造を理解するための、 様々なアプローチについて、解説する予定です。
くみひもの数理 鈴木 武史
様々な色に染められた糸を交差させて組み上げる「くみひも」は、 ここ京都でも栄えた伝統工芸です。 くみひも職人は単純な工程を巧みに組み合わせて複雑な柄を組んでゆきますが、 数学者はこうした工程を「演算」や「作用」といった言葉を用いて解釈し、 くみひもの集合を「群」(演算を持った集合)として研究してきました。 講義では、この「くみひも群」について紹介し、 さらに、この素朴で一見単純な対象が、 位相幾何や統計力学等、数理科学の様々な分野の問題と絡み合い、 深い結果に結び付いている様子をお話したいと思っています。
劣モジュラ構造と離散凸性 藤重 悟
グラフやネットワークなどの離散システムに現れる劣モジュラ構造について論じます。 劣モジュラ構造は、 劣モジュラ関数と呼ばれるある種の集合関数とそれに付随して定義される多面体によって表現され、 効率よく解くことができる多くの組合せ最適化に顔をのぞかせます。 本講義では、 いくつかの具体例を通して劣モジュラ構造の本質とその面白さを伝え、 「劣モジュラ関数の理論」と、 近年、室田一雄によって展開されてきた「離散凸解析」への入門のお話をします。
2004年8月2日-8月5日(第26回)
この結び目はほどけるか? 大槻 知忠
ひもを結ぶと結び目ができます。 結び方をかえると、できる結び目もさまざまです。 では、どれくらい多様な結び目があるのでしょうか? 変形して互いにうつりあう結び目を同じ結び目とみなして、 数学的対象として結び目を研究する分野を結び目理論といいます。 与えられた結び目が同じであることを示すのは比較的簡単で、 すなわち、実際にそれらを変形してみせることによって同じ結び目は同じであるとわかります。 ちがう結び目が確かにちがうということを示すのは比較的難しく、 これを示すときに不変量というものがつかわれます。 この講義では、結び目のいろいろな不変量がどのように構成されるのかを解説します。 幾何的な量をいかに離散化して代数的にとりだしてくるのかという工夫に不変量のおもしろさがあるとおもいます。
円周率の公式と計算法 大浦 拓哉
円周率の計算は、アルキメデスの時代から現代にいたるまで、 さまざまな人たちによって行われてきています。 その計算公式と計算法には、その時代の高度な数学が用いられてきました。 この講義では、円周率の計算法を中心とするさまざまな数学的話題について解説する予定です。
不変式の話 向井 茂
2次方程式 ax2+2bx+c=0の判別式D=4(b2-ac)はよく知られている。判別式は高次の方程式にも一般化され、それが消えること(D=0)で重解の存在が特徴付けられる。 19世紀にBooleは方程式の係数の多項式の中で特殊1次変換でもって不変なものの全体を調べ、2次方程式や3次方程式では実質的に判別式しかないことを示した。しかし、4次以上の方程式ではこれは成立しない。多くの数学者の努力により方程式の不変式はよく解明され、一般の不変式研究の雛形となった。また、その研究過程からいくつかの重要な数学的概念も誕生している。より幾何的な例や具体的な計算を交えながら不変式論を説明してゆきたい。
2003年8月4日-8月7日(第25回)
大気と海の流体力学 山田 道夫
地球や惑星の大きなスケールの流体運動は、回転や重力の影響を受けるため日常身の回りの流れとは違った性質を持ち、しかもこれら奇妙な性質は天気の移り変わりや海流の道筋と直接に関わります。ここでは、これらの性質を紹介し、流体方程式との関わりについて説明したいと思います。現象への数理的アプローチと考え方、架空の惑星についての考察などを解説する予定です。
行列で表現する話 有木 進
連立方程式を解くとは、 $f_1(x_1,\dots,x_n)=0, \cdots, f_r(x_1,\dots,x_n)=0$ をみたす「数の組」 $x=(x_1,\dots,x_n)$ を求めることですが、ここでは $x_1,\dots,x_r$ が同じサイズの正方行列であるとし、関係式 $f_1(x_1,\dots,x_n)=0, \cdots, f_r(x_1,\dots,x_n)=0$ をみたす「行列の組」を求めることを考えましょう。このような問題は表現論という分野で考えられてきました。原理的にはどんな関係式を考えてもいいのですが、実際に研究されているのは数学や物理で自然に現れる関係式、つまり応用の見込めそうな筋のいい関係式だけです。 この講義では、線形代数で出てきた行列の標準形を表現論の見方で捉えなおすことから始めて、現代の表現論の一端をお見せするところまでご案内したいと思います。
複素解析と平面図形たち 山ノ井 克俊
複素数から複素数への関数で微分可能なものを正則関数と呼びます。この定義は普通の実微分可能関数、つまり高校数学に登場する実数から実数への微分可能な関数、の素直な拡張です。しかし、正則関数の世界では実微分可能関数の世界とはかなり趣のちがう、独特で見事な現象に出会うことができます。この講座の目標は、正則関数の世界にある「幾何」をいくつかの有名な定理を通して感じとって頂くことです。実微分可能関数との性質の違いが際だち、そこが面白い、という題材を選ぶ予定です。
テキスト pdf [1.4Mb]
2002年8月5日-8月8日(第24回)
自己言及の論理と計算 長谷川 真人
自分自身について述べることの難しさと面白さは、日常誰でも経験することだと思います。 この講座では、数理論理学と計算機科学の密接な関係を示す好例として、自己言及から生じる様々なパラドックスなどの数理論理学における問題、また自分自身を呼び出すような再帰的なプログラムやデータ構造に関する問題などについて、統一的な視点から考察します。
積分の周期について 齋藤 恭司
円周率 \pi = 3,141592 ... (以下無限に続く)は円周の長さとして、積分 \frac{\pi}{2} = \int^{1}_{0}\frac{dx}{\sqrt{1-x^{2}}} で与えられます。\pi の様に超越的な数が右辺の様に、高々根号の入る積分で表示されるのは非常に面白いと思います。積分を不定積分にすると \sin ^{-1}(t) = \int \frac{dx}{\sqrt{1-x^{2}}} 三角函数の逆函数 (2\pi はその周期)となります。ガウスは更に、不定積分 \int \frac{dx}{\sqrt{1-x^{4}}} を考察して、複素変数の2重の周期函数(楕円函数の特別な場合)を得ました。この講義では積分の周期、又その高次元化等について考えてみたいと思います。
トーリックの世界 藤野 修
ユークリッド空間内の有限個のベクトルで張られた凸体を錐と呼びます。錐の集まりである扇が今回のお話の主人公です。扇から自然にトーリック多様体という代数多様体が構成できます。トーリック多様体の視点を導入することにより代数幾何の理論を扇の研究に用いることが出来ます。 一方、森理論は高次元代数幾何学の中心であり、現在も活発に研究されている大変難しい分野です。一般の代数多様体の世界ではまだまだ完成には程遠い状態です。しかしトーリック多様体の世界では森理論は扇の分割という非常に素朴な話になります。 講義では多面体や扇の分割という素朴なお話を題材にし、皆さんを広大なトーリック幾何学の世界の入口まで案内したいです。
2001年8月6日-8月10日(第23回)
電気回路とランダムウォーク 熊谷 隆
皆さんの中には、高校の物理でオームの法則・キルヒホッフの法則といった、電気回路についての法則を経験則として学んだ人も多いと思います。この講座では、これらの法則が離散調和解析と呼ばれる数学を用いてどのように表現されるかを学び、電気回路に対応するランダムウォーク(マルコフ連鎖)について考察します。グラフの上に電気回路を構成してそのポテンシャル論的な性質を学ぶとともに、電気回路の性が、対応するランダムウォークの性質にどのように反映するかを調べ、これらを用いた応用にも触れる予定です。
流体力学と流体数学 岡本 久
わが国の大学の数学教室では流体力学を講義することは少ないが、ヨーロッパの大学では数学教室で流体力学を教えることも多い. イギリスなどでは応用数学のかなりの部分を流体力学周辺で占めていることもある. 歴史的に見ても、 B. Riemann, H. Poincare, H. Weyl, A. N. Kolmogorov など、その人の主要な業績からは外れるけれども重要な流体力学の論文を書いてきた数学者は多い。 本講義の目的は、流体力学が数学の問題の宝庫であることを、具体例を通じて感じとっていただくことである。簡単な微分方程式は使うけれども、内容の大部分はグラフや流れの画像等を使って理解できるようにする予定である。
超弦理論の数学 高橋 篤史
物質や空間の基本構成要素が「点(素粒子)」ではなく1次元の空間的な広がりを持った「弦」であると考えることから, 超弦理論は始まりました. 現在では, 一般相対性理論と量子論の究極的統一理論, つまり万物の理論の最有力候補として, 理論物理学の表舞台で活躍しています. 数学と理論物理学は互いに刺激を与えながら発展してきましたが, 超弦理論はこれまで以上に数学の世界に非常に大きな影響を与え続けています. それは, 群論・表現論・保型形式・数論・代数幾何・シンプレクティック幾何・・・と広範囲にわたりますが, それも「弦」の持つ1次元の空間的自由度が理由です. この講座では, 超弦理論の数学的側面について, 入門的解説および最新の成果の紹介をします. とくに, 「空間とは何か」という幾何学の基本的問題に対する超弦理論からのアプローチについて触れたいと思います.
2000年7月31日-8月4日(第22回)
球面の対称性 永田 雅嗣
「対称性」というのは、実生活にもなじみの深い概念です。「球面という図形にどんな対称性があるか」と問われれば、誰でも点対称、回転対称、面対称などのアイデアを思い起こすでしょう。 では、点対称や面対称が必ず周期2の対称性であるのは、なぜでしょうか。「周期3の点対称」のようなものがありえないことの理由をつきつめて考えていくと、図形のグローバルな性質をつかさどる、美しい数学が見えてきます。図形の定性的な性質と、定量的な群論とを結ぶ、変換群論と呼ばれる幾何理論を紹介したいと思います。
有理点の問題と符号暗号への応用について 伊原 康隆
代数曲線の有理点が符号、暗号(主に符号)の問題にどのように使われるかについて、入門的な話をしたいと思います。 体、とくに有限体とは何か(?)といったあたりから話をはじめ、代数曲線とその有理点、楕円曲線の場合、等についての基礎的な話をし、それらが符号、暗号に関する如何なる問題にどう応用されるかについて、その一端を紹介したいと思います。
離散と連続 - 微分方程式の数値解析 降旗 大介
「数えられるもの=離散量」と「数えられないもの=連続量」という素朴な感覚にたがわず、数学では離散量と連続量は異なった扱いを受けます。 しかし、離散と連続の間には、連続は離散の極限であるという直感を越えて微妙で意義深い関係があるらしいことが各分野の様々な結果によって強く示唆されていて、非常に興味深いものがあります。 本講座では、そうした離散と連続の関係の一端を紹介するべく、離散量を対象としアルゴリズムの構築と計算量の解析を柱とする計算機科学と、連続量を対象とし関数空間の解析を柱とする関数解析学とが合流する分野 - 微分方程式の数値解析 - を中心に講演を行います。
1999年8月2日-8月6日(第21回)
多項式の解の近似がとりもつ数論と幾何の関係 望月 新一
多項式の有理数解の研究は、歴史が長いだけに、樣々なアプロ-チを産み出しているが、二十世紀の後半に開発され、現在では数々の輝かしい成果を挙げているアプロ-チとして、現代数論幾何がある。本講義の目標は、その現代数論幾何の世界を紹介することにある。現代数論幾何の基本は、標語的にいえば、多項式の解の近似にあるといってもよい。つまり、有理数というものは、整数論の対象としては構造が複雑すぎるため、数論的にはより単純な構造をした実数や複素数のような数で近似することによって多項式の有理数解を調べるのである。このような近似解のなす集合は、有理数解のなす集合と違い、「滑らかな物質」で出来た幾何的な対象をなしていて、その対象の幾何的性質が、有理数解の性質に大きく影響することが知られている。
計算幾何学入門 田村 明久
平面上に与えられた有限個の点の集合に対して、これを含む最小の凸多角形を求める問題を(2次元)凸包問題とよびます。計算幾何学とは、このような幾何的な問題を解くアルゴリズム(解法)を 研究する計算機科学の一分野です。 本講座では、凸包問題のほかに勢力圏のモデルとして利用されるボロノイ図など、計算幾何学において基礎的な問題とそれらに対するアルゴリズムを紹介します。また、アルゴリズムの効率性の評価についてもふれます。
微積分をつうじて多様体が見える 宮岡 洋一
「多様体」は現代数学を理解する上で鍵となる概念です。 数学のなかでも最も古い伝統をもつ幾何学は、三次元空間という入れ物にはいっている図形という素朴な直感から出発したわけですが、百五十年ほど前のこと、リ-マンは、必ずしも入れ物を必要とせず、いくらでも高い次元をもてる、多様体の概念に到達しました。この概念は解析学を複雑な図形のなかで自由に展開することを可能とし、その結果として宇宙全体の幾何構造といったものまで考察することまでできるようになったのです。 この講義では、多様体の豊かな世界への入門として、積分を通じて解析(微分形式)と幾何(コホモロジ-)とがかかわりあう、その様子に焦点をしぼって解説したいと思います。
1998年8月3日-8月7日(第20回)
永田 誠
竹井 義次
西村 進
1997年8月4日-8月8日(第19回)
中山 昇
森 正武
河合 俊哉
1996年8月5日-8月9日(第18回)
Jacques Garrigue
古田 幹雄
高橋 陽一郎
1995年8月7日-8月11日(第17回)
p進数と整数論
辻 雄
谷口 雅治
岩田 覚
1994年8月8日-8月12日(第16回)
代数曲線の幾何
森 重文
大堀 淳
玉川 安騎男
1994年3月14日-3月17日
「非線形現象のモデリングとその数理」大学院生以上を対象
生体系と非平衡過程
都甲 潔
生態学と時・空間パターン
重定 南奈子
電気回路と力学系
川上 博
流体の乱れ
岡本 久
化学反応と非線形性非平衡系
吉川 研一
1993年8月3日-8月6日(第15回)
服部 隆志
織田 孝幸
大木谷 耕司
1992年8月4日-8月13日(第14回)
楠岡 成雄
室田 一雄
小嶋 泉
松本 眞
1991年8月6日-8月15日(第13回)
伊原 康隆
磯 祐介
ナビエ・ストークス流の話
木田 重雄
萩谷 昌己
1990年
開催しませんでした
1989年7月25日-8月3日(第12回)
松浦 重武
一松 信
楠岡 成雄
成木 勇夫
1988年8月2日-8月11日(第11回)
松浦 重武
三輪 哲二
島田 信夫
一松 信
1987年8月11日-8月20日(第10回)
齋藤 恭司
笠原 晧司
一松 信
南 政次
1986年
開催しませんでした
1985年7月24日-8月1日(第9回)
四元数の話
荒木 不二洋
一松 信
松浦 重武
笠原 晧司
1984年7月24日-8月2日(第8回)
一松 信
松浦 重武
廣中 平祐
岩井 齊良
1983年(第7回)
一松 信
宇敷 重広
中西 襄
松浦 重武
1982年(第6回)
廣中 平祐
一松 信
ミクロの論理
荒木 不二洋
松浦 重武
1981年
開催しませんでした
1980年(第5回)
一松 信
上田 ヨシ亮
松浦 重武
後藤 金英
1979年(第4回)
小松 醇郎
松浦 重武
伊藤 清
一松 信
1978年(第3回)
高須 達
伊藤 清
廣中 平祐
山口 昌哉
1977年(第2回)
松浦 重武
複素数と物理学
荒木 不二洋
記号列の数理
西尾 英之助
一松 信
1976年(第1回)
松浦 重武
数学と自然科学
佐藤 幹夫
シンメトリー(対称性)の話
吉澤 尚明
島田 信夫
伊藤 清
